早教吧作业答案频道 -->数学-->
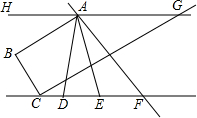
如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG.(1)求∠EAG的度数;(2)求证:HG∥CF;(3)试判断∠DAE与∠AFC之间的数量关系,并说明理由.
题目详情
如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG.
(1)求∠EAG的度数;
(2)求证:HG∥CF;
(3)试判断∠DAE与∠AFC之间的数量关系,并说明理由.

(1)求∠EAG的度数;
(2)求证:HG∥CF;
(3)试判断∠DAE与∠AFC之间的数量关系,并说明理由.
▼优质解答
答案和解析
(1)∵∠BAH=30°,
∴∠BAG=180°-30°=150°,
∵AE平分∠BAG,
∴∠EAG=
∠BAG=75°;
(2)∵AB⊥CB,垂足为B,CG⊥BC,垂足为C,
∴AB∥CG,
∴∠AGC=∠HAB=30°,
∵∠BAH=∠GCF=30°,
∴∠AGC=∠GCF,
∴HG∥CF;
(3)∠AFC=2∠DAE,
理由:设∠DAE=x,∠EAF=y,
∵AD平分∠BAF,AE平分∠BAG,
∴∠BAE=∠GAE,∠BAD=∠FAD=x+y,
∴x+y+x=y+∠GAF,
∴∠GAF=2x=2∠DAE,
∵HG∥CF,
∴∠AFC=∠GAF,
∴∠AFC=2∠DAE.
∴∠BAG=180°-30°=150°,
∵AE平分∠BAG,
∴∠EAG=
| 1 |
| 2 |
(2)∵AB⊥CB,垂足为B,CG⊥BC,垂足为C,
∴AB∥CG,
∴∠AGC=∠HAB=30°,
∵∠BAH=∠GCF=30°,
∴∠AGC=∠GCF,
∴HG∥CF;
(3)∠AFC=2∠DAE,
理由:设∠DAE=x,∠EAF=y,
∵AD平分∠BAF,AE平分∠BAG,
∴∠BAE=∠GAE,∠BAD=∠FAD=x+y,
∴x+y+x=y+∠GAF,
∴∠GAF=2x=2∠DAE,
∵HG∥CF,
∴∠AFC=∠GAF,
∴∠AFC=2∠DAE.
看了 如图,已知AB⊥CB,垂足为...的网友还看了以下:
画出下面句子中划线字的正确读音。一天,雷锋出差(A、chāB、chāi),踏(A、táB、tà)上 2020-04-08 …
平行四边形ABCD,向量AB=a,向量AD=b,H、M是AD,DC的中点,F在BC上……望高人相助 2020-05-16 …
已知f(X)=Lg1-X/1+X,a,b属于(-1,1)求证:f(a)+f(B)=F(A+B)/1 2020-05-22 …
这3个土方开挖公式分别适用在什么情况下的?刚开始做结算,V=(a+2c+kh)*(b+2c+kh) 2020-06-10 …
进制换算(213)D=()B=()H=()O(69.625)D=()D=()B=()O(127)D 2020-07-19 …
如表是元素周期表的一部分,有关说法中正确的是()ⅠAⅡAⅢAⅣAⅤAⅥAVⅡA二abc三defgh 2020-07-23 …
已知A={a,b,c,d,e,f},B={b,d,e,g,h},求A交集B,A并集B. 2020-07-30 …
该地质演化过程的正确排序是()A.d-e-g-f-b-a-h-cB.d-g-e-a-c-h-b-fC 2020-11-04 …
在以下性质的比较中,正确的是()A.微粒半径:Li+<O2-<F-<Na+B.电负性:F>N>O>C 2020-11-26 …
1)设f(x)在[a,b]上可微,且f(a)=f(b)=0,证明:在(a,b)内存在一点ξ,使f'( 2020-12-28 …