早教吧作业答案频道 -->数学-->
如图,菱形ABCD中,∠A=60°,连接BD,∠PBQ=60°,将∠PBQ绕点B任意旋转,交边AD,CD分别于点E、F(不与菱形的顶点重合),设菱形ABCD的边长为a(a为常数)(1)△ABD和△CBD都是三角形
题目详情
如图,菱形ABCD中,∠A=60°,连接BD,∠PBQ=60°,将∠PBQ绕点B任意旋转,交边AD,CD分别于点E、F(不与菱形的顶点重合),设菱形ABCD的边长为a(a为常数)
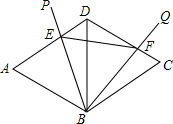
(1)△ABD和△CBD都是___三角形;
(2)判断△BEF的形状,并说明理由;
(3)在运动过程中,四边形BEDF的面积是否变化,若不变,求出其面积的值(用a表示);若变化,请说明理由.
(4)若a=3,设△DEF的周长为m,直接写出m的取值范围.

(1)△ABD和△CBD都是___三角形;
(2)判断△BEF的形状,并说明理由;
(3)在运动过程中,四边形BEDF的面积是否变化,若不变,求出其面积的值(用a表示);若变化,请说明理由.
(4)若a=3,设△DEF的周长为m,直接写出m的取值范围.
▼优质解答
答案和解析
(1)∵四边形ABCD是菱形,
∴AD=AB=BC=CD,∠C=∠A=60°
∴△ABD和△CBD都是等边三角形;
故答案为:等边;
(2)△BEF是等边三角形,
理由:由(1)知,△ABD和△CBD都是等边三角形,
∴∠EDB=∠DBC=∠C=60°,BD=BC
∵∠EBF=60°,
∴∠EBD=∠CBF,
在△BDE与△BCF中,
,
∴△BDE≌△BCF,
∴BE=BF,
∴△BEF是等边三角形;
(3)不变,
理由:∵△ABD是等边三角形,AB=a,
∴AB边上的高=
a,
∴S△ABD=
a2,
∵△BDE≌△BCF,
∴S四边形BFDE=S△ABD=
a2,
∴在运动过程中,四边形BEDF的面积不变化;
(4)∵△BDE≌△BCF,
∴DE=CF,
∴DF+DE=DF+CF=3,
∵△BEF是等边三角形,
∴BF=EF,
∵BF<3,
∴△DEF的周长<6,
当BF⊥CD时,BF=
,
∴△DEF的周长=3+
,
∴m的取值范围是3+
≤m<6.
∴AD=AB=BC=CD,∠C=∠A=60°
∴△ABD和△CBD都是等边三角形;
故答案为:等边;
(2)△BEF是等边三角形,
理由:由(1)知,△ABD和△CBD都是等边三角形,
∴∠EDB=∠DBC=∠C=60°,BD=BC
∵∠EBF=60°,
∴∠EBD=∠CBF,
在△BDE与△BCF中,
|
∴△BDE≌△BCF,
∴BE=BF,
∴△BEF是等边三角形;
(3)不变,
理由:∵△ABD是等边三角形,AB=a,
∴AB边上的高=
| ||
| 2 |
∴S△ABD=
| ||
| 4 |
∵△BDE≌△BCF,
∴S四边形BFDE=S△ABD=
| ||
| 4 |
∴在运动过程中,四边形BEDF的面积不变化;
(4)∵△BDE≌△BCF,
∴DE=CF,
∴DF+DE=DF+CF=3,
∵△BEF是等边三角形,
∴BF=EF,
∵BF<3,
∴△DEF的周长<6,
当BF⊥CD时,BF=
3
| ||
| 2 |
∴△DEF的周长=3+
3
| ||
| 2 |
∴m的取值范围是3+
3
| ||
| 2 |
看了 如图,菱形ABCD中,∠A=...的网友还看了以下:
紧急(30分)1.已知|a(向量)||b(向量)|,求|a向量+b向量|的最值.2.已知菱形ABC 2020-05-13 …
设A={x/x是菱形},B={x/x是矩形},求A交B不是交集吗?是不是平行四边形呢?菱形和矩形不 2020-06-08 …
(2014•崇左)下列说法正确的是()A.对角线相等的平行四边形是菱形B.有一组邻边相等的平行四边 2020-07-06 …
命题“菱形的四条边相等”的否命题是A.四条边相等的四边形是菱形B.四条边不相等的四边形不是菱形C. 2020-07-15 …
下列命题中,真命题是()A.对角线互相垂直且相等的四边形是菱形B.对角线互相垂直的平行四边形是菱形 2020-07-25 …
用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是()(摘录)A.对角线互相垂直的平 2020-07-25 …
如图:已知点M、N、P、Q分别为菱形ABCD四边上的中点,下列说法正确的是()A.四边形MNPQ是 2020-07-30 …
下列命题中,正确的是()A.有一个角是60°的平行四边形是菱形B.有一组邻边相等的四边形是菱形C. 2020-07-30 …
下列命题中,正确的是()A.有一个角是60°的平行四边形是菱形B.有一组邻边相等的四边形是菱形C. 2020-07-30 …
公路工程坡度的一点问题坡度等于tanA=a/c,设B为直角,c边为水平边,边abc分别对应角ABC, 2020-11-10 …