早教吧作业答案频道 -->数学-->
已知,如图,在Rt△ABC中,∠ACB=90°,点D是AB中点,过点D作DF⊥AC,垂足为F,过点C作AB的平行线,交DF的延长线于点E,连接CD,AE.(1)求证:四边形AECD是菱形;(2)当∠BAC的大小满足什么
题目详情
已知,如图,在Rt△ABC中,∠ACB=90°,点D是AB中点,过点D作DF⊥AC,垂足为F,过点C作AB的平行线,交DF的延长线于点E,连接CD,AE.
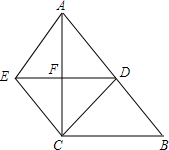
(1)求证:四边形AECD是菱形;
(2)当∠BAC的大小满足什么条件时,四边形AECD是正方形?证明你的结论.

(1)求证:四边形AECD是菱形;
(2)当∠BAC的大小满足什么条件时,四边形AECD是正方形?证明你的结论.
▼优质解答
答案和解析
(1)证明:∵∠ACB=90°,DF⊥AC,
∴DF∥BC,∵点D是AB中点,
∴F是AC的中点,
∴AF=CF,
∵CE∥AB,
∴∠ECF=∠DAF,
在△CEF和△ADF中,
,
∴△CEF≌△ADF(ASA),
∴EF=DF,
∴四边形AECD是平行四边形,
又∵DF⊥AC,
∴四边形AECD是菱形;
(2) 当∠BAC=45°时,四边形AECD是正方形;理由如下:
∵四边形AECD是菱形,
∴∠EAC=∠BAC=45°,
∴∠EAD=90°,
∴四边形AECD是正方形.
∴DF∥BC,∵点D是AB中点,
∴F是AC的中点,
∴AF=CF,
∵CE∥AB,
∴∠ECF=∠DAF,
在△CEF和△ADF中,
|
∴△CEF≌△ADF(ASA),
∴EF=DF,
∴四边形AECD是平行四边形,
又∵DF⊥AC,
∴四边形AECD是菱形;
(2) 当∠BAC=45°时,四边形AECD是正方形;理由如下:
∵四边形AECD是菱形,
∴∠EAC=∠BAC=45°,
∴∠EAD=90°,
∴四边形AECD是正方形.
看了 已知,如图,在Rt△ABC中...的网友还看了以下:
已知,如图∠A=∠C,CD丄AB于D,交AE于F,试断定ΔAEB的形状,并说明你的结论的合理性.AD 2020-03-30 …
矩阵 A 满足:AAT = E 且 |A| = -1,则矩阵 A 必有一特征值为-1.为什么等于证 2020-05-15 …
设方阵A满足A乘以A的转置等于E,且A的行列式小于1.求A+E的行列式 2020-05-16 …
依照《香港特别行政区基本法》的规定,香港特别行政区的行政长官由年满40周岁,在香港通常居住连续满 2020-06-04 …
已知:平行四边形ABCD中,对角线AC.BD相交于点O,∠AEC.∠BED都等于90°.求证∶四边 2020-06-06 …
与电源相连的平行板电容器中插入带电为Q有厚度的导体板与电源(电动势为E)相连的平行板电容器中插入带 2020-07-29 …
公共自行车问卷调查表问卷调查1、您选用自行车的原因A公交太拥挤B交通堵塞C环保D锻炼身体E出行距离短 2020-11-10 …
对下列名家书法作品鉴赏恰当的一项()A.第(1)幅是颜真卿的行书,“点画丰厚饱满,结构阔大端正”B. 2020-11-13 …
读中国地区图,回答下列各题:(1)A是省,竹楼是该省族的传统民居.(2)B的简称是,C是省,该省西部 2020-11-25 …
学校进行了一次考试,考试的科目是语文、历史、数学、物理和英语,每科满分为5分,其余等级依次为4分、3 2020-12-06 …