早教吧作业答案频道 -->数学-->
已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
题目详情
已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
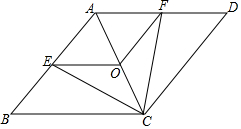
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.

(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD,
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF,OF=
DC,OE=
BC,OE∥BC,
在△BCE和△DCF中,
,
∴△BCE≌△DCF(SAS);
(2) 当AB⊥BC时,四边形AEOF是正方形,理由如下:
由(1)得:AE=OE=OF=AF,
∴四边形AEOF是菱形,
∵AB⊥BC,OE∥BC,
∴OE⊥AB,
∴∠AEO=90°,
∴四边形AEOF是正方形.
∴∠B=∠D,AB=BC=DC=AD,
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF,OF=
| 1 |
| 2 |
| 1 |
| 2 |
在△BCE和△DCF中,
|
∴△BCE≌△DCF(SAS);
(2) 当AB⊥BC时,四边形AEOF是正方形,理由如下:
由(1)得:AE=OE=OF=AF,
∴四边形AEOF是菱形,
∵AB⊥BC,OE∥BC,
∴OE⊥AB,
∴∠AEO=90°,
∴四边形AEOF是正方形.
看了 已知:如图,在菱形ABCD中...的网友还看了以下:
1、已知,映射A={1,2,3},B={4,5,6},f:A→B满足1是4的一个原象,这样的映射共 2020-05-23 …
f(x)是定义在R上的函数,且对任意实数x,y都有f(x+y)=f(x)+f(y)-1成立,当f( 2020-06-02 …
设在区间[0,1]上f''(x)>0,则f'(0)f'(1)和f(1)-f(0)的大小顺序是设在区 2020-06-08 …
已知函数F(X)在R上可导,其导函数为F(X),若F(X)满足:(x-1)[f'(x)-F(X)] 2020-06-12 …
已知函数fx满足:对任意x,y∈R,都有f(x+y)=f(x)f(y)-f(x)-f(y)+2成立 2020-06-12 …
几道高中函数题(求详解)1.已知函数f(X)=ax²+bx+c满足f(1)=f(4),则()A.f 2020-07-05 …
设函数f(x)对任意函数x,y,有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,求f 2020-12-08 …
已知函数f(x)=ax3+x2+bx(a,b∈R,且F(x)=f(x)+3ax2+2x+b为奇函数. 2020-12-08 …
已知f(x)在R上是增函已知f(x)在R上是增函数,a,b∈R,且a+b≤0,则有[]A、f(a)+ 2020-12-08 …
已知函数f(x)的定义域是(0,正无穷),且对一切x>0,y>0都有f(x/y)=f(x)-f(y) 2021-01-23 …