如图，在Rt△ABC中，∠BAC=90°，现在有一足够大的直角三角板，它的直角顶点D是BC上一点，另两条直角边分别交AB、AC于点E、F．（1）如图1，若DE⊥AB，DF⊥AC，求证：四边形AEDF是矩形；（2）在

Question

如图，在Rt△ABC中，∠BAC=90°，现在有一足够大的直角三角板，它的直角顶点D是BC上一点，另两条直角边分别交AB、AC于点E、F．
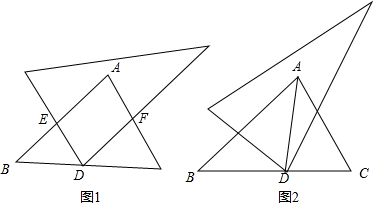
（1）如图1，若DE⊥AB，DF⊥AC，求证：四边形AEDF是矩形；
（2）在（1）条件下，若点D在∠BAC的 角平分线上，试判断此时四边形AEDF的形状，并说明理由；
（3）若点D在∠BAC的角平分线上，将直角三角板绕点D旋转一定的角度，使得直角三角板的两条边与两条直角边分别交于点E、F（如图2），试证明AE+AF=√(2)AD．

Answer 1

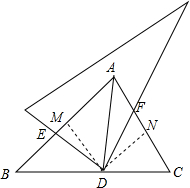（1）∵DE⊥AB，BF⊥AC，
∴∠AED=∠AFD=90°，
∵∠BAC=90°，
∴四边形AEDF是矩形；

（2）四边形AEDF是正方形，
理由：∵点D在∠BAC的 角平分线上，DE⊥AB，BF⊥AC，
∴DE=DF，
∴矩形AEDF是正方形；

（3）作DM⊥AB于M，DN⊥AC于N，
∴∠AED=∠AFD=∠BAC=90°，
∵点D在∠BAC的 角平分线上，
∴DM=DN，
∴四边形AMDN是正方形，
∴AM=DM=DN=AN，∠MDN=∠AMD=90°，
∴∠MDF+∠NDF=90°，
∵∠EDF=90°，
∴∠MDF+∠EDM=90°，
∴∠NDF=∠EDM，
在△EMD与△END中，

∠EMD=∠DNF

DM=DN

∠EDM=∠NDF

，
∴△EMD≌△END，
∴EM=FN，
∵∠AMD=90°，
∴AM²+DM²=AD²，
∴AD=√(2)AM，
∵AM=(1)/(2)（AM+AN）=(1)/(2)（AE+AF），
∴AD=√(2)×(1)/(2)（AE+AF），
∴AE+AF=√(2)AD．