如图1，在△ABC中，∠ACB=90°，BC=2，∠A=30°，点E，F分别是线段BC，AC的中点，连结EF．（1）线段BE与AF的位置关系是，

Question

如图 1 ，在 △ ABC 中， ∠ ACB=90° ， BC=2 ， ∠ A=30° ，点 E ， F 分别是线段 BC ， AC 的中点，连结 EF ．

（ 1 ）线段 BE 与 AF 的位置关系是 　 　 ， = 　　 ．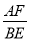

（ 2 ）如图 2 ，当 △ CEF 绕点 C 顺时针旋转 a 时（ 0° ＜ a ＜ 180° ），连结 AF ， BE ，（ 1 ）中的结论是否仍然成立．如果成立，请证明；如果不成立，请说明理由．

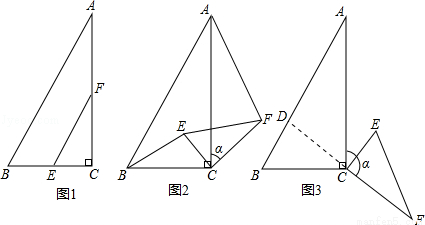
（ 3 ）如图 3 ，当 △ CEF 绕点 C 顺时针旋转 a 时（ 0° ＜ a ＜ 180° ），延长 FC 交 AB 于点 D ，如果 AD=6 - 2 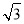，求旋转角 a 的度数．

 

 

Answer 1

(1) 线段BE与AF的位置关系是互相垂直；；(2) （1）中结论仍然成立．证明见解析；（3）135°．

分 析：
（1）结合已知角度以及利用锐角三角函数关系求出AB的长，进而得出答案；（2）利用已知得出△BEC∽△AFC，进而得出∠1=∠2，即可得出答案；（3）过点D作DH⊥BC于H，则DB=4-（6-2）=2-2，进而得出BH=-1，DH=3-，求出CH=BH，得出∠DCA=45°，进而得出答案．试题
解析：
（1）如图1，线段BE与AF的位置关系是互相垂直；∵∠ACB=90°，BC=2，∠A=30°，∴AC=2，∵点E，F分别是线段BC，AC的中点，∴=；（2）（1）中结论仍然成立．证明：如图2，∵点E，F分别是线段BC，AC的中点，∴EC=BC，FC=AC，∴，∵∠BCE=∠ACF=α，∴△BEC∽△AFC，∴，∴∠1=∠2，延长BE交AC于点O，交AF于点M∵∠BOC=∠AOM，∠1=∠2∴∠BCO=∠AMO=90°∴BE⊥AF；（3）如图3，∵∠ACB=90°，BC=2，∠A=30°∴AB=4，∠B=60°过点D作DH⊥BC于H∴DB=4-（6-2）=2-2，∴BH=-1，DH=3-，又∵CH=2-（-1）=3-，∴CH=BH，∴∠HCD=45°，∴∠DCA=45°，∴α=180°-45°=135°．
考点：
几何变换综合题．