早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=90°,点G是△ABC的重心,且AG⊥CG,CG的延长线交AB于H.(1)求证:△CAG∽△ABC;(2)求S△AGH:S△ABC的值.
题目详情
如图,在△ABC中,∠ACB=90°,点G是△ABC的重心,且AG⊥CG,CG的延长
线交AB于H.
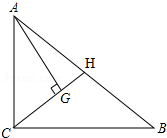
(1)求证:△CAG∽△ABC;
(2)求S△AGH:S△ABC的值.
线交AB于H.

(1)求证:△CAG∽△ABC;
(2)求S△AGH:S△ABC的值.
▼优质解答
答案和解析
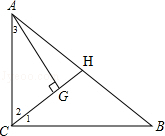 (1)证明:如图,设GH=a,
(1)证明:如图,设GH=a,
∵点G是△ABC的重心,
∴CG=2HG=2a,CH为AB边上的中线,
∴CH=AH=BH=3a,
∴∠1=∠3,
∵AG⊥CG,
∴∠2+∠3=90°,
而∠1+∠2=90°,
∴∠1=∠3,
∴∠B=∠3,
而∠ACB=∠AGC=90°,
∴△CAG∽△ABC;
(2)∵点G是△ABC的重心,
∴CG=2HG,
∴HG=
CH,
∴S△AHG=
S△ACH,
∵CH为AB边上的中线,
∴S△ACH=
S△ABC,
∴S△AHG=
×
S△ABC,
∴S△AGH:S△ABC=1:6.
 (1)证明:如图,设GH=a,
(1)证明:如图,设GH=a,∵点G是△ABC的重心,
∴CG=2HG=2a,CH为AB边上的中线,
∴CH=AH=BH=3a,
∴∠1=∠3,
∵AG⊥CG,
∴∠2+∠3=90°,
而∠1+∠2=90°,
∴∠1=∠3,
∴∠B=∠3,
而∠ACB=∠AGC=90°,
∴△CAG∽△ABC;
(2)∵点G是△ABC的重心,
∴CG=2HG,
∴HG=
| 1 |
| 3 |
∴S△AHG=
| 1 |
| 3 |
∵CH为AB边上的中线,
∴S△ACH=
| 1 |
| 2 |
∴S△AHG=
| 1 |
| 3 |
| 1 |
| 2 |
∴S△AGH:S△ABC=1:6.
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
物质的量浓度为amol/ml的S溶液(体积不限),要配置成质量分数为b%的S溶液,H毫升(ml), 2020-05-14 …
三角形ABC的三边abc和面积S满足S=c^2-(a-b)^2,且,求面积S的最大面积(^2)是指 2020-05-17 …
A.πA,B,C (σB=B(R×S))B.πR.A,R.B,R.C (σR.B=S.B (R×S) 2020-05-26 …
给定关系模式R(A.B,C,D)、S(C,D,E),与语句如下:A.A.C. S.C B.A.,B, 2020-05-26 …
§43(a)oftheLanhamAct,15U.S.C.§1125(a)(1).这种法律英语的编 2020-06-04 …
锐角△ABC的三边a,b,c和面积S满足条件S=[c^2-(a-b)^2]/4k,又角C既不是△A 2020-06-05 …
急,在线等已知AB:DB=AC:EC,且AE:EC=3:4,BD-AD=7,求AD长已知AB:DB= 2020-11-21 …
水流过A管后,分两支向B、C两管流去.已知A、B、C三管的横截面积分别为S(A)=100cm2、S( 2020-12-03 …
联系上下文,完成对话.1.A:Hello!Nina.B:Hello,Nina.ThisisMike. 2020-12-05 …
利用发波水槽得到的水面波形如图a、b所示,则()A.图a、b均显示了波的干涉现象B.图a、b均显示了 2020-12-25 …