我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心。重心有很多美妙的性质，如有关线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形

Question

我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心。重心有很多美妙的性质，如有关线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形中的若干问题。

请你利用重心的概念完成如下问题：

        

      

 

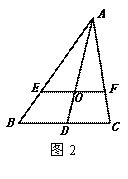
（ 1 ）如图 1 ，△ ABC 的中线 AD 、 CE 的交点 O 为三角形的重心， 利用三角形的中位线 可以证明： ，请你完成该证明；

（ 2 ）运用第（ 1 ）的结论解决以下问题：

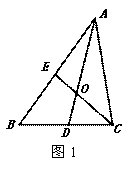
①小丽说：“过三角形的重心任画一条直线都能将三角形的面积平分”。小 明想了想说：“这个说法是错误的。”他过点 O 画出了 BC 的平行线，交 AB 、 AC 于点 E 、 F ，如图 2 ，你能求出 的值吗？谁的说法正确？

②△ ABC 中， ∠ C ＝ 90° ， AB=6cm ，求△ ABC 的重心与外心的距离。

Answer 1

（ 1 ）连 DE ，                            ……………………………………… 1 分

由题意， D 、 E 为 BC 、 AB 中点，

      ∴ DE 为△ ABC 的中位线，

      ∴ DE ∥ AC ， DE= AC 。

      ∴△ ODE ∽△ OAC ，且相似比为 1:2 ，      ……………………………………… 2 分

      ∴ AO=2OD ∴ ……………………………………………………………… 3 分

（ 2 ）①∵ EF ∥ BC ，∴△ AEO ∽△ ABD ，相似比为 。

    ∴ ………………………………………………………………………… 4 分

        同理，△ AEF ∽△ ABC ，相似比为 ……………………………………………… 5 分

       ∴ ，∴ …………………………………………………… 6 分

       ∴小明说法正确。………………………………………………………………… 7 分

② Rt △ ABC 外心为 AB 的中点，记为点 D ，……………………………………… 8 分

     则 CD= AB=3 ，………………………………………………………………… 9 分

     重心 O 在中线 CD 上，由 (1)

     ∴ OD=3 × =1. …………………………………………………………………… 10 分