早教吧作业答案频道 -->数学-->
如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?()A.1B.2C.23-2D.4-23
题目详情
如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )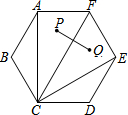
A. 1
B. 2
C. 2
-23
D. 4-23
▼优质解答
答案和解析
如图,
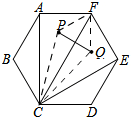
连接PF,QF,PC,QC,
∵P、Q两点分别为△ACF、△CEF的内心
∴四边形FPCQ是筝形,
∴PQ⊥CF,
∵△ACF≌△ECF,且内角是30°,60°,90°的三角形,
∴AC=
,AF=2
,CF=2AF=4,
∴PQ=2×
=2+2
-4
=2
-2.
故选C.

连接PF,QF,PC,QC,
∵P、Q两点分别为△ACF、△CEF的内心
∴四边形FPCQ是筝形,
∴PQ⊥CF,
∵△ACF≌△ECF,且内角是30°,60°,90°的三角形,
∴AC=
| 3 |
| 3 |
∴PQ=2×
| AF+AC-CF |
| 2 |
=2+2
| 3 |
=2
| 3 |
故选C.
看了 如图,正六边形ABCDEF中...的网友还看了以下:
在边长为5a+4(a>0)的正方形中,截去两个边长分别为3a+1与2a+2的小正方行,试求剩余部分的 2020-03-30 …
已解决物体A.B的质量分别为6,4,A与B.B与地面之间的动摩擦因数都为0.3,在外力的作用下,A 2020-04-09 …
物体A.B的质量分别为6,4,A与B.B与地面之间的动摩擦因数都为0.3,在外力的作用下,A与B一 2020-04-09 …
.计算题..急有两个实心圆柱体A和B叠放在一起,并且完全接触(A在B的正中上面),已知AB两个圆柱 2020-04-27 …
如果直角三角形的一条边为2,4,a.那么a的取值可以有几个?A.0个B.1个C.2个D.3个 2020-05-21 …
假设A资产的预期收益率为10%,标准差为8.7%;B资产的预期收益率为8%,标准差为8.4%,A和B 2020-05-22 …
若直角三角形的三边长为2,4,a,求a的平方? 2020-06-03 …
如果直角三角形三条边的三边长为2,4,a,则a的取值可以有(a为奇数)()A.0个;B.1个;C. 2020-06-03 …
A,B,C三件衬衫的总价格为520元A、B、C三件衬衫的总价格为520元,若分别按9.5折、9折、 2020-06-22 …
下列句子中,句式相同的是()1莫之夭阏者2耕植不足以自给3胡为乎遑遑欲何之4去以六月息者也5彼且恶 2020-07-02 …