早教吧作业答案频道 -->数学-->
如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影为A1B1的中点O,AC=BC=AA1,∠ACB=90°(1)求证:AB⊥CC1;(2)若CO=22,求点C到平面ABO的距离.
题目详情
如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影为A1B1的中点O,AC=BC=AA1,∠ACB=90°
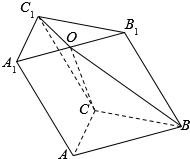
(1)求证:AB⊥CC1;
(2)若CO=
,求点C到平面ABO的距离.

(1)求证:AB⊥CC1;
(2)若CO=
| ||
| 2 |
▼优质解答
答案和解析
(1)证明:∵点C在平面A1B1C1内的射影为A1B1的中点O,AC=BC
∴CO⊥A1B1,C1O⊥A1B1,
∵CO∩C1O=O,
∴A1B1⊥平面C1OC,
∵CC1⊂平面C1OC,
∴A1B1⊥CC1,
∵AB∥A1B1,
∴AB⊥CC1;
(2) 设AC=a,
∵AC=BC=AA1,∠ACB=90°,CO=
,
∴a2=
+
a2,
∴a=1,
∴S△ABC=
设点C到平面ABO的距离为h,则
∵S△OAB=
×
×1=
,
∴由等体积可得
×
h=
×
×
,
∴h=
.
∴CO⊥A1B1,C1O⊥A1B1,
∵CO∩C1O=O,
∴A1B1⊥平面C1OC,
∵CC1⊂平面C1OC,
∴A1B1⊥CC1,
∵AB∥A1B1,
∴AB⊥CC1;
(2) 设AC=a,
∵AC=BC=AA1,∠ACB=90°,CO=
| ||
| 2 |
∴a2=
| 1 |
| 2 |
| 1 |
| 2 |
∴a=1,
∴S△ABC=
| 1 |
| 2 |
设点C到平面ABO的距离为h,则
∵S△OAB=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
∴由等体积可得
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴h=
| 1 |
| 2 |
看了 如图,在三棱柱ABC-A1B...的网友还看了以下:
a乘根号下负的1/a等于?过程!说的清楚点 2020-04-06 …
不等式数学题目,高二的1.(a-1)(a-2)(a-3)(a-4)>1202.(x^2+2x-2) 2020-05-13 …
选什么这道题如果0小于a小于二分之一,则下列不等式总成立的是Alog(1-a)大于1Bloga(1 2020-05-13 …
下图为蒙古一月、七月均温图。完成下列问题。1.P地的气温年较差大约为2.根据七月均温分布特点,推测 2020-05-13 …
写出画线部分读音与其他三个不同的单词.e的1.A.helpB.chessC.tentD.child 2020-05-14 …
是关于差的.1.A与B的差.是A-B还是B-A,或者两个都是?2.A与B的差为2.B为A+2还是A 2020-05-15 …
选出()里读音与其他不同的1.A.c(a)meraB.m(a)nC.h(a)rd2.A.(ea)s 2020-05-22 …
设nA代表阿伏加德罗常数(NA)的数值,下列说法正确的是 A.22.4 L Cl2中含有nA个C12 2020-05-25 …
不难的1:a、b为锐角,且满足sina=√5/5cosb=√10/10则a+b为多少2:设0 2020-06-06 …
哥德巴赫猜想中的1+11+22+3 2020-06-09 …