早教吧作业答案频道 -->数学-->
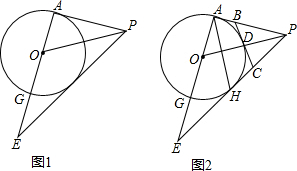
如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.(1)求证:直线PE是O的切线;(2)在图2中,设PE与O相切于点H,连结AH,点D是O的劣弧AH上一点,过
题目详情
如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.
(1)求证:直线PE是 O的切线;
(2)在图2中,设PE与 O相切于点H,连结AH,点D是 O的劣弧
上一点,过点D作 O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=
,求EH的长.
(1)求证:直线PE是 O的切线;
(2)在图2中,设PE与 O相切于点H,连结AH,点D是 O的劣弧
 |
| AH |
| 1 |
| 2 |

▼优质解答
答案和解析
证明:(1)如图1,
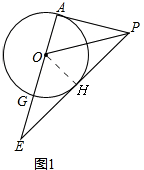
作OH⊥PE,
∴∠OHP=90°,
∵∠PAE=90,
∴∠OHP=∠OAP,
∵PO是∠APE的角平分线,
∴∠APO=∠EPO,
在△PAO和△PHO中
,
∴△PAO≌△PHO,
∴OH=OA,
∵OA是 O的半径,
∴OH是 O的半径,
∵OH⊥PE,
∴直线PE是 O的切线.
(2)如图2,连接GH,
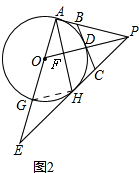
∵BC,PA,PB是 O的切线,
∴DB=DA,DC=CH,
∵△PBC的周长为4,
∴PB+PC+BC=4,
∴PB+PC+DB+DC=4,
∴PB+AB+PC+CH=4,
∴PA+PH=4,
∵PA,PH是 O的切线,
∴PA=PH,
∴PA=2,
由(1)得,△PAO≌△PHO,
∴∠OFA=90°,
∴∠EAH+∠AOP=90°,
∵∠OAP=90°,
∴∠AOP+∠APO=90°,
∴∠APO=∠EAH,
∵tan∠EAH=
,
∴tan∠APO=
=
,
∴OA=
PA=1,
∴AG=2,
∵∠AHG=90°,
∵tan∠EAH=
=
,
∵△EGH∽△EHA,
∴
=
=
=
,
∴EH=2EG,AE=2EH,
∴AE=4EG,
∵AE=EG+AG,
∴EG+AG=4EG,
∴EG=
AG=
,
∵EH是 O的切线,EGA是 O的割线,
∴EH2=EG×EA=EG×(EG+AG)=
×(
+2)=
,
∴EH=
.

作OH⊥PE,
∴∠OHP=90°,
∵∠PAE=90,
∴∠OHP=∠OAP,
∵PO是∠APE的角平分线,
∴∠APO=∠EPO,
在△PAO和△PHO中
|
∴△PAO≌△PHO,
∴OH=OA,
∵OA是 O的半径,
∴OH是 O的半径,
∵OH⊥PE,
∴直线PE是 O的切线.
(2)如图2,连接GH,

∵BC,PA,PB是 O的切线,
∴DB=DA,DC=CH,
∵△PBC的周长为4,
∴PB+PC+BC=4,
∴PB+PC+DB+DC=4,
∴PB+AB+PC+CH=4,
∴PA+PH=4,
∵PA,PH是 O的切线,
∴PA=PH,
∴PA=2,
由(1)得,△PAO≌△PHO,
∴∠OFA=90°,
∴∠EAH+∠AOP=90°,
∵∠OAP=90°,
∴∠AOP+∠APO=90°,
∴∠APO=∠EAH,
∵tan∠EAH=
| 1 |
| 2 |
∴tan∠APO=
| OA |
| PA |
| 1 |
| 2 |
∴OA=
| 1 |
| 2 |
∴AG=2,
∵∠AHG=90°,
∵tan∠EAH=
| GH |
| AH |
| 1 |
| 2 |
∵△EGH∽△EHA,
∴
| EG |
| EH |
| EH |
| AE |
| GH |
| AH |
| 1 |
| 2 |
∴EH=2EG,AE=2EH,
∴AE=4EG,
∵AE=EG+AG,
∴EG+AG=4EG,
∴EG=
| 1 |
| 3 |
| 2 |
| 3 |
∵EH是 O的切线,EGA是 O的割线,
∴EH2=EG×EA=EG×(EG+AG)=
| 2 |
| 3 |
| 2 |
| 3 |
| 16 |
| 9 |
∴EH=
| 4 |
| 3 |
看了 如图1,在△APE中,∠PA...的网友还看了以下:
已知圆O的半径为1,点P与O的距离为d,且方程“埃克斯”-2“埃克斯”+d=0有实数根,则点P在圆 2020-04-27 …
已知⊙O的半径为4cm,A为线段OP的中点,当OP=7cm时,点A与⊙O的位置关系是()A.点A在 2020-04-27 …
(2014•崇明县二模)在⊙O中,圆心O在坐标原点上,半径为210,点P的坐标为(4,个),那么点 2020-05-17 …
如图,⊙O的直径AB=4,∠ABC=30°,BC=43,D是线段BC的中点.(1)试判断点D与⊙O 2020-06-04 …
如图,在Rt△ABC中∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径 2020-07-21 …
直线AB经过圆O的圆心,与圆O相交于点AB,点C在圆O上,且角AOC=30°,点P是直线AB上的一 2020-07-26 …
⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是()A. 2020-07-26 …
开口向下的抛物线经过原点O和点E(4,0),顶点P到x轴的距离为4.点A(a,0)是线段OE上一点 2020-07-29 …
已知同一平面内存在O和点P,点P与O上的点的最大距离为8,最小距离为2,则O的半径为. 2020-07-30 …
(2012•淮安)如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0). 2020-11-01 …