早教吧作业答案频道 -->数学-->
如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.(1)求证:∠DAG=∠ABE;(2)①求证:点H总在以AB为直径的圆弧上;②画出点H所在的圆弧,并说明这
题目详情
如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.
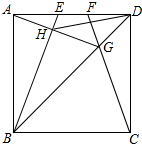
(1)求证:∠DAG=∠ABE;
(2)①求证:点H总在以AB为直径的圆弧上;
②画出点H所在的圆弧,并说明这个圆弧的两个端点字母;
(3)直接写出线段DH长度的最小值.

(1)求证:∠DAG=∠ABE;
(2)①求证:点H总在以AB为直径的圆弧上;
②画出点H所在的圆弧,并说明这个圆弧的两个端点字母;
(3)直接写出线段DH长度的最小值.
▼优质解答
答案和解析
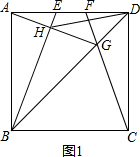 (1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
(1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
在△ADG和△CDG中,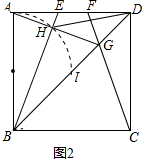
,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCF,
∴∠DAG=∠ABE;
(2)①如图1,∵∠DAG=∠ABE,∠BAH+∠DAG=∠BAD=90°,
∴∠ABE+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴BE⊥AG,
∴点H总在以AB为直径的圆弧上;
②如图2,以AB的中点O为圆心,OA长为半径画弧,交BD于I(I是BD的中点),弧的两个端点为A和I.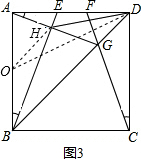
(3)如图3,取AB的中点O,连接OH、OD,
则OH=AO=
AB=2cm,
在Rt△AOD中,OD=
=
=2
,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD-OH=2
-2.
 (1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
(1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,在△ABE和△DCF中,
|
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
在△ADG和△CDG中,

|
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCF,
∴∠DAG=∠ABE;
(2)①如图1,∵∠DAG=∠ABE,∠BAH+∠DAG=∠BAD=90°,
∴∠ABE+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴BE⊥AG,
∴点H总在以AB为直径的圆弧上;
②如图2,以AB的中点O为圆心,OA长为半径画弧,交BD于I(I是BD的中点),弧的两个端点为A和I.

(3)如图3,取AB的中点O,连接OH、OD,
则OH=AO=
| 1 |
| 2 |
在Rt△AOD中,OD=
| OA2+AD2 |
| 22+42 |
| 5 |
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD-OH=2
| 5 |
看了 如图,正方形ABCD的边长为...的网友还看了以下:
如图所示,在底边长为L,顶角为120°的等腰三角形a、b、c所围区域内有磁感应强度为B,方向垂直纸 2020-04-05 …
如图所示,在x轴上方有匀强电场,场强为E;在x轴下方有匀强磁场,磁感应强度为B,方向如图,在x轴上 2020-05-13 …
x轴上方匀强磁场磁感应强度为B,方向垂直xoy平面向里,x轴下方匀强磁场磁感应强度为B/2,方向垂 2020-05-17 …
如图,三角形ABC中,点D是AB边的中点,点E是AC边上的一点,且AE=3EC,O为DC与BE的交 2020-06-19 …
如图所示,质量为m的金属棒,搁在光滑导轨的右端,导轨间距为L,距离地面高度为h,处于大小为B,方向 2020-06-22 …
三峡大坝从6月1日开始下闸蓄水,如果平均每天流入库区的水量为a立方米,平均每天流出的水量控制为b立 2020-07-10 …
一飞机相对于空气的速度大小为200km/h,风速为56km/h,方向由西向东.地面雷达站测的飞机相 2020-07-11 …
有一匀强磁场区域,区域的上下边界MM′、NN′与水平面平行,磁场的磁感应强度为B,方向如图所示,磁 2020-07-31 …
如图所示,水平地面上方的H高区域内有匀强磁场,水平界面PP′是磁场的上边界,磁感应强度为B,方向是 2020-07-31 …
如图所示,在坐标系xOy中,第一象限内充满着两个匀强磁场a和b,OP为分界线,在区域a中,磁感应强度 2020-11-01 …