早教吧作业答案频道 -->数学-->
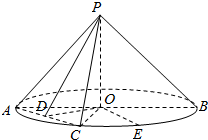
如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=22.(1)求证PO⊥AC;(2)求二面角P-AC-E的平面角的余弦值.
题目详情
如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2
.

(1)求证PO⊥AC;
(2)求二面角P-AC-E的平面角的余弦值.
| 2 |

(1)求证PO⊥AC;
(2)求二面角P-AC-E的平面角的余弦值.
▼优质解答
答案和解析
 证明:(1)∵PO是圆锥的高,∴PO⊥底面圆O,
证明:(1)∵PO是圆锥的高,∴PO⊥底面圆O,
又AC⊂底面圆O,
∴PO⊥AC.
(2)取AC中点为D,连接PD、OD,又圆锥母线PA=PC,∴PD⊥AC
∵底面圆O上OA=OC∴OD⊥AC
又E为劣弧CB的中点即有E∈底面圆O
∴二面角P-AC-E的平面角即为∠PDO
∵C为半圆弧AB的中点,∴∠AOC=90°
又直径AB=2
∴OD=
AC=1
∵PO⊥底面圆O 且OD⊂底面圆O,∴PO⊥OD
又PO=
,∴Rt△POD中,PD=
.
∴cos∠PDO=
=
即为所求.
 证明:(1)∵PO是圆锥的高,∴PO⊥底面圆O,
证明:(1)∵PO是圆锥的高,∴PO⊥底面圆O,又AC⊂底面圆O,
∴PO⊥AC.
(2)取AC中点为D,连接PD、OD,又圆锥母线PA=PC,∴PD⊥AC
∵底面圆O上OA=OC∴OD⊥AC
又E为劣弧CB的中点即有E∈底面圆O
∴二面角P-AC-E的平面角即为∠PDO
∵C为半圆弧AB的中点,∴∠AOC=90°
又直径AB=2
| 2 |
| 1 |
| 2 |
∵PO⊥底面圆O 且OD⊂底面圆O,∴PO⊥OD
又PO=
| 2 |
| 3 |
∴cos∠PDO=
| OD |
| PD |
| ||
| 3 |
看了 如图,圆锥的底面圆心为O,直...的网友还看了以下:
“春天孩子面,一日三朝变”。阅读今年3月1日至17日上海地区气温曲线图,分析回答下面几题。小题1: 2020-04-09 …
下面两图均为极地俯视图,读图完成下面20~21题。20.甲地在乙地的A.西南方向B.东南方向C.西 2020-05-13 …
读下面两个岛屿图,回答下面试题。甲岛位于乙岛的A.西南方向B.东北方向C.东南方向D.西北方向甲、 2020-05-13 …
平行六面体ABCD-A´B´C´D´的六个面都是菱形,那么顶点B在平面ACB´上的射影一定是⊿AC 2020-05-13 …
下面说法正确的是()A.面积相等的两个三角形,底和高不一定相等B.三角形的面积等于平行四边形的一半 2020-05-13 …
面积最接近120平方厘米的物品表面是()A.面值100元人民币的正面B.数学书的封面C.1元硬币的 2020-05-17 …
下面是小明"探究物体漂浮在液面的条件"的实验步骤,其顺序是打乱的.A.测出试管和沙子的重力;B.把 2020-06-07 …
图书馆在邮局的北面,少年宫在邮局的南面,少年宫在图书馆的[]A.东面B.西面C.南面D.北面 2020-06-16 …
“一战”期间,我国民族工业发展最快的行业是[]A.面粉业与榨油B.烟草业与火柴C.化工业与钢铁D. 2020-06-16 …
伟大的民族精神体现在方方面面。例如A.面对外敌入侵,中华民族同仇敌忾,奋起抗争B.在无数自然灾害面 2020-06-22 …