早教吧作业答案频道 -->数学-->
如图,▱ABCD的边AD与经过A、B、C三点的⊙O相切(1)求证:弧AB=弧AC(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E=1213,求tan∠D的值
题目详情
如图,▱ABCD的边AD与经过A、B、C三点的⊙O相切
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E=
,求tan∠D的值
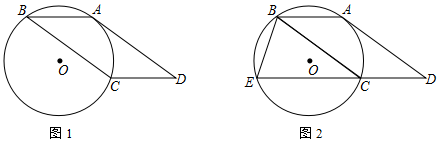
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E=
| 12 |
| 13 |
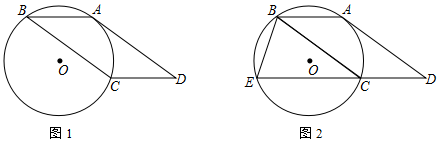
▼优质解答
答案和解析
(1)证明:连接OA交BC于F.
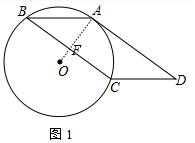
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠CFO,
∵AD是⊙O的切线,
∴∠OAD=90°,
∴∠OFC=90°,
∴OF⊥BC,
∴OA平分
,
即
=
.
(2) 如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.
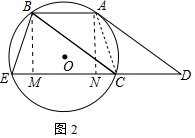
∵四边形ABCD是平行四边形,
∴∠D=∠ABC=∠BCE,
∴
=
,
∵
=
,
∴
=
=
,
∴BE=AB=AC,
=
,
∴∠E=∠ACE,
在Rt△BEM中,sin∠E=
,设BE=13m,则BM=12m,EM=5m,
在Rt△ANC中,sin∠ACN=sin∠E=
,AC=EB=13m,则CN=5m,
∵BM=CN,BM∥CN,
∴四边形BMNA是平行四边形,
∴MN=AB=EB=13m,
∴CM=18m,
∴tan∠BCE=
=
=
,
∴tan∠D=
.

∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠CFO,
∵AD是⊙O的切线,
∴∠OAD=90°,
∴∠OFC=90°,
∴OF⊥BC,
∴OA平分
 |
| BC |
即
 |
| AB |
 |
| AC |
(2) 如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.

∵四边形ABCD是平行四边形,
∴∠D=∠ABC=∠BCE,
∴
 |
| EB |
 |
| CA |
∵
 |
| BA |
 |
| AC |
∴
 |
| EB |
 |
| CA |
 |
| BA |
∴BE=AB=AC,
 |
| EA |
 |
| CB |
∴∠E=∠ACE,
在Rt△BEM中,sin∠E=
| 12 |
| 13 |
在Rt△ANC中,sin∠ACN=sin∠E=
| 12 |
| 13 |
∵BM=CN,BM∥CN,
∴四边形BMNA是平行四边形,
∴MN=AB=EB=13m,
∴CM=18m,
∴tan∠BCE=
| BM |
| CM |
| 12m |
| 18m |
| 2 |
| 3 |
∴tan∠D=
| 2 |
| 3 |
看了 如图,▱ABCD的边AD与经...的网友还看了以下:
读经纬网图,回答2--4题.2.图中是东西半球分界线的经线是()3.图中最长的纬线是()4.关于M 2020-04-23 …
用边长为一的小正方形按下图的方式拼成大长方形.(第一个有两个正方形,第二个有三个正方形,第三个有5 2020-05-17 …
图没.是这样的:第一个图为九宫格,第二个为二十五宫格,第三个为四十九宫格.以此类推,问:计算第n个 2020-06-10 …
观察下列砌钢管的横截面图:则第n个图的钢管数是(用含n的式子表示) 2020-06-19 …
观察下列砌钢管的横截面图,它们是按一定规律排列的,依照此规律,第n个图的钢管数是(用含n的式子表示 2020-06-19 …
观察下列砌钢管的横截面图:则第n个图的钢管数是.(用含n的式子表示) 2020-06-19 …
阅读下列语段,把其中加点字的注音和拼音所表示的汉字依次填在方格内。清河的柳,是心的色相。敞开胸膛, 2020-06-26 …
该图为116°E经线的一段L。读图完成问题。小题1:经线L段最可能跨越的纬度是()A.20°N至2 2020-07-18 …
如图是甲国、乙国本土的轮廓图,读图完成下列要求.(1)如果经度每隔15°时间相差1小时,M、N两地的 2020-11-11 …
单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个 2020-11-28 …