早教吧作业答案频道 -->数学-->
在平面直角坐标系中,A、B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2x+y-4=0相切,则圆C面积的最小值为.
题目详情
在平面直角坐标系中,A、B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2x+y-4=0相切,则圆C面积的最小值为___.
▼优质解答
答案和解析
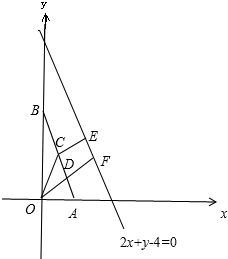 如图,设AB的中点为C,坐标原点为O,圆半径为r,
如图,设AB的中点为C,坐标原点为O,圆半径为r,
由已知得|OC|=|CE|=r,
过点O作直线2x+y-4=0的垂直线段OF,
交AB于D,交直线2x+y-4=0于F,
则当D恰为OF中点时,圆C的半径最小,即面积最小.
此时圆的直径为O(0,0)到直线2x+y-4=0的距离为:
d=
=
,
此时r=
d=
∴圆C的面积的最小值为:Smin=π×(
)2=
.
故答案为
.
 如图,设AB的中点为C,坐标原点为O,圆半径为r,
如图,设AB的中点为C,坐标原点为O,圆半径为r,由已知得|OC|=|CE|=r,
过点O作直线2x+y-4=0的垂直线段OF,
交AB于D,交直线2x+y-4=0于F,
则当D恰为OF中点时,圆C的半径最小,即面积最小.
此时圆的直径为O(0,0)到直线2x+y-4=0的距离为:
d=
| |-4| | ||
|
| 4 | ||
|
此时r=
| 1 |
| 2 |
| 2 | ||
|
∴圆C的面积的最小值为:Smin=π×(
| 2 | ||
|
| 4π |
| 5 |
故答案为
| 4π |
| 5 |
看了 在平面直角坐标系中,A、B分...的网友还看了以下:
在平面直角坐标系中xOy中,O(0,0),A(1,1),B(2,0),直线ax+by=1与线段OA 2020-05-13 …
(1/2)在三角形ABC中,AG垂直于BC于点G,以A为直角顶点,分别以AB、AC为直角边,向三角 2020-06-15 …
如图,CD是⊙O的直径,点A是半圆上的三等分点,B是弧AD的中点,P点为直线CD上的一个动点,当C 2020-06-19 …
一块普通铁板,长50cm宽40cm.长的方向两头固定不动,垂直于铁板的力为30T,受力面积为直径1 2020-07-11 …
一个体重为500N的同学骑自行车上学,在水平路面上匀速行驶.有关数据是:自行车净重为200N,行驶 2020-07-12 …
如图,一长度为10的线段AC的两个端点A、C分别在y轴和x轴的正半轴上滑动,以A为直角顶点,AC为 2020-07-24 …
已知椭圆C的右焦点为F2(2,0),实轴的长为42.(1)求椭圆C的标准方程;(2)过点F1(-2 2020-07-30 …
(1)小球在最高点所受的洛伦兹力f;(2)小球的初速度v0.如图所示,一根水平光滑的绝缘直槽轨连接一 2020-11-24 …
英语翻译原文:本文给出的类圆周假设基于一个犯罪圆周,即以系列杀人案件中地理位置最远的两起案件连接的直 2020-12-01 …
长度测量是最基本的测量之一,除常规测量方法外还有“累积法”、“化曲为直”、“悬绳法”、“等量代换法” 2021-01-07 …