早教吧作业答案频道 -->数学-->
过圆外一点P作圆的两条切线和一条割线,切点为A,B,所作割线交圆于C,D两点,C在P,D之间,在弦CD上取一点Q,使∠DAQ=∠PBC.求证:∠DBQ=∠PAC.
题目详情
过圆外一点P作圆的两条切线和一条割线,切点为A,B,所作割线交圆于C,D两点,C在P,D之间,在弦CD上取一点Q,使∠DAQ=∠PBC.求证:∠DBQ=∠PAC.
▼优质解答
答案和解析
如图所示,
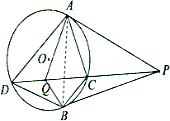
连接AB,∵△PBC∽△PDB,
∴
=
,
同理
=
;
又PA=PB,
∴
=
,即
=
;
又∠BAC=∠PBC=∠DAQ,
∴∠BAC=∠ADQ,
∴△ABC∽ADQ,
∴
=
,
∴
=
,
又∠DAQ=∠DBC=∠BDQ,
∴△ADQ∽△DBQ,
∴∠ADQ=∠DBQ=∠PAC.

连接AB,∵△PBC∽△PDB,
∴
| BD |
| BC |
| PD |
| PB |
同理
| AD |
| AC |
| PD |
| PA |
又PA=PB,
∴
| BD |
| BC |
| AD |
| AC |
| BD |
| AD |
| BC |
| AC |
又∠BAC=∠PBC=∠DAQ,
∴∠BAC=∠ADQ,
∴△ABC∽ADQ,
∴
| BC |
| AC |
| DQ |
| AQ |
∴
| BD |
| AD |
| DQ |
| AQ |
又∠DAQ=∠DBC=∠BDQ,
∴△ADQ∽△DBQ,
∴∠ADQ=∠DBQ=∠PAC.
看了 过圆外一点P作圆的两条切线和...的网友还看了以下:
初中数学综合题(相似形)如图,在RT三角形ABC中,角A=90度,AB=8,AC=6,D,E为AB 2020-04-26 …
如图,在RT△ABC中.∠A=90°,AB=6,AB=8,D,E分别是边AB,AC的中点,点P从点 2020-05-13 …
如图所示,一带正电的粒子以一定的初速度v0沿两板的中线进入水平放置的平行金属板内,恰好沿下板的边缘 2020-05-13 …
电容器带电量问题金属球A与同心球壳B组成电容器,(B半径比A大,在A外)球A上带电荷q,壳B上带Q 2020-05-16 …
如图所示,在O点置一点电荷Q,以O为圆心作一圆.现将一试探电荷q从A分别移到圆上的B、C、D三点, 2020-05-21 …
当电量一定时,场强E=U/d=Q/Cd=4πkdQ/εSd=4πkQ/εS,由此可见E与Q/εS成 2020-06-12 …
如图所示,在倾角为θ的粗糙斜面上放置与轻弹簧相连的物体A,弹簧另一端通过轻绳连接到轻质定滑轮Q上, 2020-06-12 …
如图所示,水平面上A、B两点相距8m,滑块P静止在A点,质量mQ=0.6kg的滑块Q过B点时具有方 2020-06-16 …
如用,一半径为R的圆盘上均匀分布着电荷量为Q的电荷,在垂直于圆盘且过圆心d的轴线上有a、b、c、e四 2020-11-26 …
关于电容器的电容C、电压U和所带电荷量Q之间的关系,以下说法正确的是()A.C由U确定B.C由Q确定 2020-11-29 …