早教吧作业答案频道 -->数学-->
如图,AH是O的直径,AE平分∠FAH,交O于点E,过点E的直线FG⊥AF,垂足为F,B为半径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.(1)求证:直线FG是O的切线;(2)若CD=10,EB=5,求O的直径
题目详情
如图,AH是 O的直径,AE平分∠FAH,交 O于点E,过点E的直线FG⊥AF,垂足为F,B为半径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.
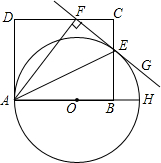
(1)求证:直线FG是 O的切线;
(2)若CD=10,EB=5,求 O的直径.

(1)求证:直线FG是 O的切线;
(2)若CD=10,EB=5,求 O的直径.
▼优质解答
答案和解析
(1)如图1,连接OE,
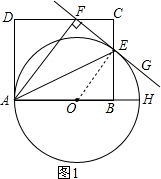
∵OA=OE,
∴∠EAO=∠AEO,
∵AE平分∠FAH,
∴∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
∵AF⊥GF,
∴∠AFE=∠OEF=90°,
∴OE⊥GF,
∵点E在圆上,OE是半径,
∴GF是 O的切线.
(2)∵四边形ABCD是矩形,CD=10,
∴AB=CD=10,∠ABE=90°,
设OA=OE=x,则OB=10-x,
在Rt△OBE中,∠OBE=90°,BE=5,
由勾股定理得:OB2+BE2=OE2,
∴(10-x)2+52=x2,
∴x=
,
AH=2×
=
,
∴ O的直径为
.

∵OA=OE,
∴∠EAO=∠AEO,
∵AE平分∠FAH,
∴∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
∵AF⊥GF,
∴∠AFE=∠OEF=90°,
∴OE⊥GF,
∵点E在圆上,OE是半径,
∴GF是 O的切线.
(2)∵四边形ABCD是矩形,CD=10,
∴AB=CD=10,∠ABE=90°,
设OA=OE=x,则OB=10-x,
在Rt△OBE中,∠OBE=90°,BE=5,
由勾股定理得:OB2+BE2=OE2,
∴(10-x)2+52=x2,
∴x=
| 25 |
| 4 |
AH=2×
| 25 |
| 4 |
| 25 |
| 2 |
∴ O的直径为
| 25 |
| 2 |
看了 如图,AH是O的直径,AE平...的网友还看了以下:
一道java编程题:有一矩阵:a b c d e f g h i j k l m n o p q 2020-04-06 …
求教工程数学线性代数1若n阶矩阵A为正交矩阵,则A必为可逆矩阵且A-1=A'2若Rank(A)=n 2020-04-12 …
从斜角为45度的固定斜面B点正上方,据B点高度为h的A点处,静止释放一个质量为m的弹性小球,落在B 2020-05-13 …
数学的问题已知△ABC中,BC=a,BC边上的高AH=h;矩形DEFG的定点D,E在边BC上,定点 2020-05-14 …
如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB 2020-05-16 …
matlab中用牛顿下山法求方程的根想用牛顿下山法求一个含有一个未知数w的方程的根.假如矩阵为A, 2020-05-17 …
如图所示的装置是在竖直平面内放置的绝缘轨道,处于水平向右的匀强电场中,以带负电荷的小球从高h的A处 2020-05-17 …
在高度为H的桌面上以速度v0水平抛出质量为m的物体,当物体落到距地面高为h的A点时,速度为v,如图 2020-06-14 …
(2010•南通模拟)如图所示的装置是在竖直平面内放置光滑的绝缘轨道,处于水平向右的匀强电场中,一 2020-06-15 …
如图所示,物块m由高h的A处静止释放后沿斜面运动到B,再沿水平面运动后停在C处,已知物块与斜面及水 2020-06-16 …