早教吧作业答案频道 -->数学-->
如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D(1)求证:四边形CDEF是平行四边形;
题目详情
如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
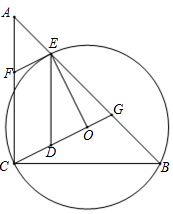
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.

(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.
▼优质解答
答案和解析
(1)连接CE,
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠B=45°,
∵EF是⊙O的切线,
∴∠FEC=∠B=45°,∠FEO=90°,
∴∠CEO=45°,
∵DE∥CF,
∴∠ECD=∠FEC=45°,
∴∠EOC=90°,
∴EF∥OD,
∴四边形CDEF是平行四边形;
(2)过G作GN⊥BC于N,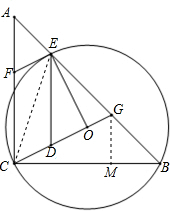
∴△GMB是等腰直角三角形,
∴MB=GM,
∵四边形CDEF是平行四边形,
∴∠FCD=∠FED,
∵∠ACD+∠GCB=∠GCB+∠CGM=90°,
∴∠CGM=∠ACD,
∴∠CGM=∠DEF,
∵tan∠DEF=2,
∴tan∠CGM=
=2,
∴CM=2GM,
∴CM+BM=2GM+GM=3,
∴GM=1,
∴BG=
GM=
.
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠B=45°,
∵EF是⊙O的切线,
∴∠FEC=∠B=45°,∠FEO=90°,
∴∠CEO=45°,
∵DE∥CF,
∴∠ECD=∠FEC=45°,
∴∠EOC=90°,
∴EF∥OD,
∴四边形CDEF是平行四边形;
(2)过G作GN⊥BC于N,

∴△GMB是等腰直角三角形,
∴MB=GM,
∵四边形CDEF是平行四边形,
∴∠FCD=∠FED,
∵∠ACD+∠GCB=∠GCB+∠CGM=90°,
∴∠CGM=∠ACD,
∴∠CGM=∠DEF,
∵tan∠DEF=2,
∴tan∠CGM=
| CM |
| GM |
∴CM=2GM,
∴CM+BM=2GM+GM=3,
∴GM=1,
∴BG=
| 2 |
| 2 |
看了 如图,在△ABC中,AC=B...的网友还看了以下:
由短周期元素组成的A、B、C、D、E、F六种微粒由短周期元素组成的A,B,C,D,E,F六种微粒, 2020-04-08 …
考研数学倒数部分设F(x)=g(x)t(x),t(x)在t=a连续不可导,又g'(a)存在,则g( 2020-05-17 …
请问您可以帮我完成《近似代数》中的几道难题吗?设G是个交换群,证明H={g┃g∈G,g4=e}是G 2020-06-10 …
线性代数问题A是n阶矩阵,A2-2A+E=0得到A=E对不?还是A=E是前式的充分非必要条件?帮忙 2020-06-12 …
为什麽元音中的e在单词中读æ像bed的音标[bed]e是读æ但a[e]是读e音老师教的也是e音但为 2020-07-09 …
一道大学导数题设F(x)=g(x)f(x),f(x)在x=a处连续,但不可导,又g'(a)存在,则 2020-07-15 …
python组合问题有一个二维数列list=[['a','b'],['c','d','e'],'f 2020-07-17 …
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的 2020-07-31 …
G=(V,E)是一个图,若G中每个顶点度数均大于等于3,试证明不存在有7条边的连通简单平面图. 2020-08-01 …
为什么A^-1*(A,E)是初等行变换A^-1等于有限个初等方阵相乘我知道,但是初等行变换不是应该 2020-08-02 …