早教吧作业答案频道 -->数学-->
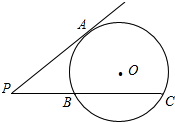
如图所示,O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P是O外一点,过点P作O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与O的交点.若PA,PB,PC的长都
题目详情
如图所示, O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P是 O外一点,过点P作 O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与 O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.

▼优质解答
答案和解析
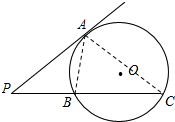 设方程x2+2(k-2)x+k=0的两个根为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②
设方程x2+2(k-2)x+k=0的两个根为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②
由题设及①知,x1,x2都是整数.从①,②消去k,得2x1x2+x1+x2=4,(2x1+1)(2x2+1)=9.
由上式知,x2≤4,且当k=0时,x2=4,故最大的整数根为4.
于是 O的直径为4,所以BC≤4.
因为BC=PC-PB为正整数,所以BC=1,2,3或4.
连接AB,AC,因为∠PAB=∠PCA,所以△PAB∽△PCA,
=
.
故PA2=PB(PB+BC)③
(1)当BC=1时,由③得,PA2=PB2+PB,于是PB2<PA2<(PB+1)2,矛盾!
(2)当BC=2时,由③得,PA2=PB2+2PB,于是PB2<PA2<(PB+1)2,矛盾!
(3)当BC=3时,由③得,PA2=PB2+3PB,于是(PA-PB)(PA+PB)=3PB,
由于PB不是合数,结合PA-PB<PA+PB,
故只可能
,
,
,
解得PA=2,PB=1.
此时PA2+PB2+PC2=21.
(4)当BC=4,由③得,PA2=PB2+4PB,于是(PB+1)2<PB2+4PB=PA2<(PB+2)2,矛盾.
综上所述PA2+PB2+PC2=21.
 设方程x2+2(k-2)x+k=0的两个根为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②
设方程x2+2(k-2)x+k=0的两个根为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②由题设及①知,x1,x2都是整数.从①,②消去k,得2x1x2+x1+x2=4,(2x1+1)(2x2+1)=9.
由上式知,x2≤4,且当k=0时,x2=4,故最大的整数根为4.
于是 O的直径为4,所以BC≤4.
因为BC=PC-PB为正整数,所以BC=1,2,3或4.
连接AB,AC,因为∠PAB=∠PCA,所以△PAB∽△PCA,
| PA |
| PB |
| PC |
| PA |
故PA2=PB(PB+BC)③
(1)当BC=1时,由③得,PA2=PB2+PB,于是PB2<PA2<(PB+1)2,矛盾!
(2)当BC=2时,由③得,PA2=PB2+2PB,于是PB2<PA2<(PB+1)2,矛盾!
(3)当BC=3时,由③得,PA2=PB2+3PB,于是(PA-PB)(PA+PB)=3PB,
由于PB不是合数,结合PA-PB<PA+PB,
故只可能
|
|
|
解得PA=2,PB=1.
此时PA2+PB2+PC2=21.
(4)当BC=4,由③得,PA2=PB2+4PB,于是(PB+1)2<PB2+4PB=PA2<(PB+2)2,矛盾.
综上所述PA2+PB2+PC2=21.
看了 如图所示,O的直径的长是关于...的网友还看了以下:
一个圆柱的底面积半径是2分米,如果把圆柱的底面分成许多相等的扇形,然后把圆柱沿扇形的半径一一切开, 2020-04-27 …
两圆相切,自其公切线上任一点P引二直线,一线割圆于A,B,另一线割圆于C,D,求证A,B,C,D共 2020-05-13 …
我们的生命历程其实就像一条线,而且这条线一定不可能是笔直而光滑的.试着想一下,如果你的人生就是一条 2020-05-16 …
solidworks倒圆角两个面圆角半径不一致.怎么操作命令.打个比方,2个相交的AB俩面倒圆角, 2020-05-17 …
圆上的同一条线的线速度如果是圆周运动有两点处于同一条半径内,距离圆心长度不同此时是线速度相等还是角 2020-05-20 …
路由器了解到,可以用来到达目的网络三种可能的途径。一条路线是从EIGRP和具有20514560.另一 2020-05-31 …
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的 2020-06-12 …
一:有一长直截流导体,通有10A电流.试求周围介质为空气和铁磁材料(u=200)时,距导线轴心5c 2020-06-19 …
γ射线、x射线、可见光、微波都是电磁波,以下将它们按波长由大到小排序,正确的是()A.γ射线一x射 2020-06-22 …
底线①一个物欲的时代和一个非物欲的时代,人的底线是不同的。社会的底线也在下降。所谓社会底线下降,就 2020-06-26 …