如图，在四边形ABCD中，AB=AD=6cm，CB=CD=8cm，且∠B=90°，该四边形存在内切圆吗？如果存在，请计算内切圆的半径．

Question

如图，在四边形ABCD中，AB=AD=6cm，CB=CD=8cm，且∠B=90°，该四边形存在内切圆吗？如果存在，请计算内切圆的半径．

Answer 1

存在．
连接AC，作∠ABC的平分线交AC于O，作OH⊥BC于H，如图，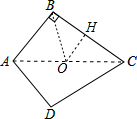
在△ABC和△ADC中，

AB=AD

CB=CD

AC=AC

，
∴△ABC≌△ADC，
∴∠BAC=∠DAC，∠ACB=∠ACD，
∴AC平分∠BAD和∠BCD，
∵OB平分∠ABC，
∴点O到四边形ABCD的各边的距离相等，
∴四边形ABCD存在内切圆，内切圆的圆心为点O，半径为OH，
∵∠ABC=90°，
∴∠OBH=45°，
∴△OBH为等腰直角三角形，
∴OH=BH，
设OH=r，则BH=r，CH=8-r，
∵OH∥AB，
∴△COH∽△CAB，
∴(OH)/(AB)=(CH)/(CB)，即(r)/(6)=(8-r)/(8)，
∴r=(24)/(7)，
即四边形ABCD的内切圆的半径为(24)/(7)．