已知点A是抛物线x2=4y的对称轴与准线的交点，点F为抛物线的焦点，P在抛物线上且满足|PA|=m|PF|，当m取最大值时|PA|的值为（）A.1B.5C.6D.22

Question

已知点A是抛物线x²=4y的对称轴与准线的交点，点F为抛物线的焦点，P在抛物线上且满足|PA|=m|PF|，当m取最大值时|PA|的值为（　　）

A. 1

B.

√(5)

C.

√(6)

D. 2

√(2)

Answer 1

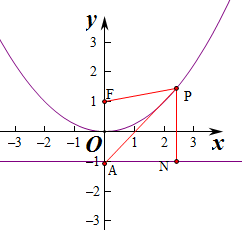抛物线的标准方程为x²=4y，
则抛物线的焦点为F（0，1），准线方程为y=-1，
过P作准线的垂线，垂足为N，
则由抛物线的定义可得|PN|=|PF|，
∵|PA|=m|PF|，∴|PA|=m|PN|，
设PA的倾斜角为α，则sinα=(1)/(m)，
当m取得最大值时，sinα最小，此时直线PA与抛物线相切，
设直线PA的方程为y=kx-1，代入x²=4y，
可得x²=4（kx-1），
即x²-4kx+4=0，
∴△=16k²-16=0，∴k=±1，
∴P（2，1），
∴|PA|=√(4+4)=2√(2)．
故选D．