抛物线y2=2px（p>0）的焦点为F，准线为L，A、B是抛物线上的两个动点，且满足∠AFB=π3．设线段AB的中点M在L上的投影为N，则|MN||AB|的最大值是（）A.23B.1C.32D.16

Question

抛物线y²=2px（p>0）的焦点为F，准线为L，A、B是抛物线上的两个动点，且满足∠AFB=

(π)/(3)．设线段AB的中点M在L上的投影为N，则(|MN|)/(|AB|)的最大值是（　　）

A.

(2)/(3)

B. 1

C.

(3)/(2)

D.

(1)/(6)

Answer 1

设|AF|=a，|BF|=b，连接AF、BF，
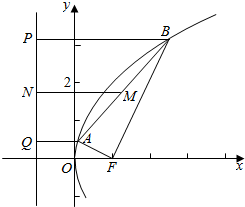
由抛物线定义，得|AF|=|AQ|，|BF|=|BP|，
在梯形ABPQ中，2|MN|=|AQ|+|BP|=a+b．
由余弦定理得，
|AB|²=a²+b²-2abcos60°=a²+b²-ab，
配方得，|AB|²=（a+b）²-3ab，
又∵ab≤（(a+b)/(2)）²，
∴（a+b）²-3ab≥（a+b）²-(3)/(4)（a+b）²=(1)/(4)（a+b）²
得到|AB|≥(1)/(2)（a+b）．
∴(|MN|)/(|AB|)≤1，
即(|MN|)/(|AB|)的最大值为1．
故选：B．