过抛物线y2=2px（p>0）的焦点F作直线与抛物线交于A，B两点，以AB为直径画圆，借助信息技术工具，观察它与抛物线准线l的关系，你能得到什么结论？相应于椭圆、双曲线如何？你能证明你

Question

过抛物线y²=2px（p>0）的焦点F作直线与抛物线交于A，B两点，以AB为直径画圆，借助信息技术工具，观察它与抛物线准线l的关系，你能得到什么结论？相应于椭圆、双曲线如何？你能证明你的结论吗？

Answer 1

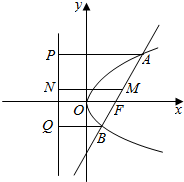取AB的中点M，分别过A、B、M作准线的垂线AP、BQ、MN，垂足分别为P、Q、N，如图所示：
由抛物线的定义可知，|AP|=|AF|，|BQ|=|BF|，
在直角梯形APQB中，|MN|=(1)/(2)（|AP|+|BQ|）=(1)/(2)（|AF|+|BF|）=(1)/(2)|AB|，
故圆心M到准线的距离等于半径，
∴以AB为直径的圆与抛物线的准线相切．
圆半径为r，则r=(1)/(2)AB，分别过点A，B做右准线的垂线，则构成一个直角梯形，两底长分别为(1)/(e)AF，(1)/(e)BF（e为离心率）
圆心到准线的距离d为梯形的中位线长即(1)/(2e)（AF+BF）
∵椭圆0<e<1，∴d=(1)/(2e)（AF+BF）=(1)/(2e)AB>(1)/(2)AB=r，∴相离
双曲线e>1，可得d<r，相交．