早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,直线l的参数方程为:(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.(Ⅰ)求曲线C的平面直角坐标方程;(
题目详情
在平面直角坐标系xOy中,直线l的参数方程为: (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为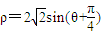 .
.
(Ⅰ)求曲线C的平面直角坐标方程;
(Ⅱ)设直线l与曲线C交于点M,N,若点P的坐标为(1,0),求|PM|•|PN|的值.
 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为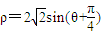 .
.(Ⅰ)求曲线C的平面直角坐标方程;
(Ⅱ)设直线l与曲线C交于点M,N,若点P的坐标为(1,0),求|PM|•|PN|的值.
▼优质解答
答案和解析
分析:
(Ⅰ)把给出的等式右边展开两角和的正弦公式,两边同时乘以ρ后代入公式x=ρcosθ,y=ρsinθ,整理即可得到答案;(Ⅱ)直接把直的参数方程代入曲线C的方程,化为关于t的一元二次方程后利用参数t的几何意义可得结论.
(Ⅰ)由,得==2sinθ+2cosθ.所以ρ2=2ρsinθ+2ρcosθ.即x2+y2-2x-2y=0.所以曲线C的平面直角坐标方程为x2+y2-2x-2y=0;(Ⅱ)由直线l的参数方程为:(t为参数),知直线l是过点P(1,0),且倾斜角为的直线,把直线的参数方程代入曲线C得,.所以|PM|•|PN|=|t1t2|=1.
点评:
本题考查了直线的参数方程,考查了简单曲线的极坐标方程,考查了直线和圆的关系,解答此题的关键是熟练掌握直线参数方程中参数的几何意义,是中档题.
分析:
(Ⅰ)把给出的等式右边展开两角和的正弦公式,两边同时乘以ρ后代入公式x=ρcosθ,y=ρsinθ,整理即可得到答案;(Ⅱ)直接把直的参数方程代入曲线C的方程,化为关于t的一元二次方程后利用参数t的几何意义可得结论.
(Ⅰ)由,得==2sinθ+2cosθ.所以ρ2=2ρsinθ+2ρcosθ.即x2+y2-2x-2y=0.所以曲线C的平面直角坐标方程为x2+y2-2x-2y=0;(Ⅱ)由直线l的参数方程为:(t为参数),知直线l是过点P(1,0),且倾斜角为的直线,把直线的参数方程代入曲线C得,.所以|PM|•|PN|=|t1t2|=1.
点评:
本题考查了直线的参数方程,考查了简单曲线的极坐标方程,考查了直线和圆的关系,解答此题的关键是熟练掌握直线参数方程中参数的几何意义,是中档题.
看了 在平面直角坐标系xOy中,直...的网友还看了以下:
一个标准椭圆,建直角坐标系,圆上面的点p与坐标O点构成线段c,线段c与x轴所构成的角为z.点p沿椭 2020-05-16 …
初中数学,在直角坐标系中,直线L:Y=,-2x+4分别交x轴点A,直线Y=X与直线L交于点B初中数 2020-06-06 …
如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动 2020-06-08 …
在平面直角坐标系中直线y=x+1和y=-¾x+3交于点A,直线y=x+1交x轴于点B,直线y=-¾ 2020-06-14 …
一道初三关于坐标系和圆的数学题,已知直线Y=-X+6与X轴交于点A,与Y轴交于点B,点P为X轴上可 2020-07-11 …
如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B.P为线段AB上一动 2020-07-19 …
如图,以等边△OAB的边OB所在直线为x轴,点O为坐标原点,使点A在第一象限建立平面直角坐标系,其 2020-07-22 …
如图,已知:⊙O1与⊙O2外切于点O,以直线O1O2为x轴,点O为坐标原点,建立直角坐标系,直线A 2020-07-31 …
公切线已知圆O1与圆O2外切于点O已知圆O1与圆O2外切于点O,其半径之比为1:3,以直线O1O2 2020-07-31 …
参数方程……直线参数方程为x=-1+t,y=t(t为参数),曲线c的极坐标方程是ρ=sinθ/1- 2020-08-02 …