早教吧作业答案频道 -->数学-->
如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=12CD,AB∥CD,CP⊥CD,M为PD的中点.(1)求证:AM∥平面PBC;(2)求证:平面BDP⊥平面PBC.
题目详情
如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=
CD,AB∥CD,CP⊥CD,M为PD的中点.
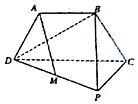
(1)求证:AM∥平面PBC;
(2)求证:平面BDP⊥平面PBC.
| 1 |
| 2 |

(1)求证:AM∥平面PBC;
(2)求证:平面BDP⊥平面PBC.
▼优质解答
答案和解析
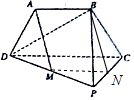 证明:(1)取PC的中点N,连结MN,BN,
证明:(1)取PC的中点N,连结MN,BN,
则MN
CD,又AB
CD,
∴四边形ABNM是平行四边形,
∴AM∥BN,又AM⊄平面PBC,BN⊂平面PBC,
∴AM∥平面PBC.
(2)∵平面ABCD⊥平面PCD,平面ABCD∩平面PCD=CD,CD⊥PC,PC⊂平面PCD,
∴PC⊥平面ABCD,∵BD⊂平面ABCD,
∴BD⊥PC,
∵四边形ABCD是等腰梯形,AD=AB=BC=
CD,
则cos∠BCD=
=
,即∠BCD=60°,
∴BD2=BC2+CD2-BC•CD=3BC2,∴BC2+BD2=CD2,
∴BD⊥BC,
又BC∩PC=C,BC⊂平面PBC,PC⊂平面PBC,
∴BD⊥平面PBC,又BD⊂平面PBD,
∴平面PBD⊥平面PBC.
 证明:(1)取PC的中点N,连结MN,BN,
证明:(1)取PC的中点N,连结MN,BN,则MN
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴四边形ABNM是平行四边形,
∴AM∥BN,又AM⊄平面PBC,BN⊂平面PBC,
∴AM∥平面PBC.
(2)∵平面ABCD⊥平面PCD,平面ABCD∩平面PCD=CD,CD⊥PC,PC⊂平面PCD,
∴PC⊥平面ABCD,∵BD⊂平面ABCD,
∴BD⊥PC,
∵四边形ABCD是等腰梯形,AD=AB=BC=
| 1 |
| 2 |
则cos∠BCD=
| ||
| BC |
| 1 |
| 2 |
∴BD2=BC2+CD2-BC•CD=3BC2,∴BC2+BD2=CD2,
∴BD⊥BC,
又BC∩PC=C,BC⊂平面PBC,PC⊂平面PBC,
∴BD⊥平面PBC,又BD⊂平面PBD,
∴平面PBD⊥平面PBC.
看了 如图,三角形PCD所在的平面...的网友还看了以下:
一张菱形硬纸板ABCD的中心是点O,沿它的一条对角线AC对折,使BO垂直于DO,这时二面角B-AC- 2020-03-30 …
把下面的式子写成(A+B)(A-B)的形式(1)(a+b+c+d)(-a-b+c+d)(2)(把下 2020-04-27 …
如果向量a,b,c共面,b,c,d也共面,那么a,b,c,d是否共面?如果不一定共面,请举例说明浪 2020-05-13 …
如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A 2020-05-13 …
请帮我解答谢谢详解某城市有a、b、c、d四个区,b、c、d三区的面积之和是a的14倍,a、c、d三 2020-06-14 …
已知::有四个人A,B,C,D各自带一顶帽子,其中有2个红色,2个黄色现在有一堵墙,A坐在墙的左面 2020-06-26 …
在平面直角坐标系xoy中,点A(1,2)B(2,1)C(4,3)若坐标平面内有一点D,使得以A,B 2020-07-31 …
在棱长为2的正方体ABCD-A'B'C'D'中,E是棱C'D'的中点,求过A.C,E,的截面EFG 2020-08-03 …
高数题目一、单选题(共10道试题,共60分。)题面见图片A.B.C.D.满分:6分2.题面见图片A. 2020-11-01 …
如图,ABCD都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B 2020-11-13 …