早教吧作业答案频道 -->数学-->
如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=π3,BC=212,点F在平面ABED内的正投影为G,且G在AE上,FG=3,点M在线段CF上,且CM=14CF.(1)证明:直线GM∥平面DEF;(2)求三棱锥M-DEF
题目详情
如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=
,BC=
,点F在平面ABED内的正投影为G,且G在AE上,FG=
,点M在线段CF上,且CM=
CF.
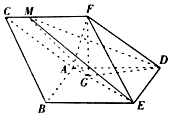
(1)证明:直线GM∥平面DEF;
(2)求三棱锥M-DEF的体积.
| π |
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 4 |

(1)证明:直线GM∥平面DEF;
(2)求三棱锥M-DEF的体积.
▼优质解答
答案和解析
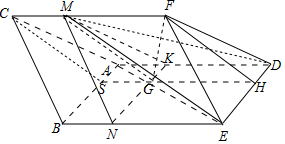
(1)证明:如图,∵面ABED是边长为2的菱形,且∠ABE=
,
∴△ABE为正三角形,且AE=2,
∵FG⊥GE,FG=
,EF=BC=
,
∴EG=
,则AG:HG=1:3,过G作SH∥AD,
交AB于S,交DE于H,
则SG:GH=1:3,
连接CS、FH,∵CM=
CF,∴CM:MF=1:3,
∴MG∥FH,又FH⊂平面DEF,MG⊄平面DEF,
∴直线GM∥平面DEF;
(2) 设过MG且平行于平面DEF的平面交三棱柱于MNK,
得三棱柱DEF-MNK,可得VM-DEF=
VDEF-KMN=VM-NEK,
∵NK=2,NE=
BE=
,∴S△NEK=
×2×
×sin
=
.
则VM-NEK=
×
×
=
.
| π |
| 3 |

∴△ABE为正三角形,且AE=2,
∵FG⊥GE,FG=
| 3 |
| ||
| 2 |
∴EG=
| 3 |
| 2 |
交AB于S,交DE于H,
则SG:GH=1:3,
连接CS、FH,∵CM=
| 1 |
| 4 |
∴MG∥FH,又FH⊂平面DEF,MG⊄平面DEF,
∴直线GM∥平面DEF;
(2) 设过MG且平行于平面DEF的平面交三棱柱于MNK,
得三棱柱DEF-MNK,可得VM-DEF=
| 1 |
| 3 |
∵NK=2,NE=
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 3 |
3
| ||
| 4 |
则VM-NEK=
| 1 |
| 3 |
3
| ||
| 4 |
| 3 |
| 3 |
| 4 |
看了 如图,三棱柱ABC-DEF中...的网友还看了以下:
已知ΔABC的内角A.B.C满足sin2A+sin(A-B已知ΔABC的内角A.B.C满足sin2 2020-06-27 …
(本小题13分)如图所示,PQ为平面的交线,已知二面角为直二面角,,∠BAP=45°.(1)证明: 2020-07-21 …
已知平面α内有一个以AB为直径的圆,PA⊥α,点C在圆周上(不同于A、B两点),点D、E分别是点A 2020-07-30 …
在平面几何里有射影定理:设△ABC的两边AB⊥AC,D是A点在BC边上的射影,则AB2=BD•BC 2020-07-30 …
如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将△ABD折起,使A点在平面BCD内的射影落 2020-07-30 …
已知i是虚数单位,m∈R,z=m(m-1)+(m2+2m-3)i.(Ⅰ)若z是纯虚数,求m的值;( 2020-08-01 …
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB=2,BC=CD=1,AB∥ 2020-10-31 …
下面使用的类比推理中恰当的是()A.“若m•2=n•2,则m=n”类比得出“若m•0=n•0,则m= 2020-11-29 …
AB为平面a内的一条斜线,B为斜足,AO丄平面a,垂足为O,直线BC在平面a内,已知∠ABC=60° 2020-12-05 …
在平面几何里有射影定理:设三角形ABC的两边AB⊥AC,D是A点在BC上的射影,则AB2=BD•BC 2020-12-25 …