早教吧作业答案频道 -->数学-->
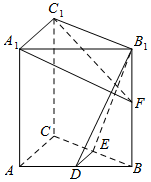
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.
题目详情
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.

(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
▼优质解答
答案和解析
(本小题满分14分)
证明:(1)∵D,E为中点,
∴DE为△ABC的中位线,∴DE∥AC,
又∵ABC-A1B1C1为棱柱,
∴AC∥A1C1,∴DE∥A1C1,
又∵A1C1⊂平面A1C1F,且DE⊄A1C1F,
∴DE∥平面A1C1F.…(6分)
(2)∵ABC-A1B1C1为直棱柱,
∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,
又∵A1C1⊥A1B1且AA1∩A1B1=A1,AA1,A1B1⊂平面AA1B1B,
∴A1C1⊥平面AA1B1B,
又A1C1∥AC∥DE,∴DE⊥平面AA1B1B,
又∵A1F⊂平面AA1B1B,∴DE⊥A1F
又∵A1F⊥B1D,DE∩B1D=D,且DE,B1D⊂平面B1DE,
∴A1F⊥平面B1DE,
又∵A1F⊂A1C1F,∴平面B1DE⊥平面A1C1F.…(14分)
证明:(1)∵D,E为中点,

∴DE为△ABC的中位线,∴DE∥AC,
又∵ABC-A1B1C1为棱柱,
∴AC∥A1C1,∴DE∥A1C1,
又∵A1C1⊂平面A1C1F,且DE⊄A1C1F,
∴DE∥平面A1C1F.…(6分)
(2)∵ABC-A1B1C1为直棱柱,
∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,
又∵A1C1⊥A1B1且AA1∩A1B1=A1,AA1,A1B1⊂平面AA1B1B,
∴A1C1⊥平面AA1B1B,
又A1C1∥AC∥DE,∴DE⊥平面AA1B1B,
又∵A1F⊂平面AA1B1B,∴DE⊥A1F
又∵A1F⊥B1D,DE∩B1D=D,且DE,B1D⊂平面B1DE,
∴A1F⊥平面B1DE,
又∵A1F⊂A1C1F,∴平面B1DE⊥平面A1C1F.…(14分)
看了 如图,在直三棱柱ABC-A1...的网友还看了以下:
我想要问问,什么时候用an,什么时候用a念书的时候说是aeiou的时候用an.但我后来发现好像有一 2020-04-08 …
A笔2元/支,B笔3元/支.某文具店准备用90元购进这两种笔,其中A笔不少于10支,B笔不少于A笔 2020-05-13 …
两桶油共重45千克,把A桶的1/6倒入B桶后,这时A桶是B桶的2/3,求A,B两桶原来各有多少千克 2020-05-13 …
选什么这道题如果0小于a小于二分之一,则下列不等式总成立的是Alog(1-a)大于1Bloga(1 2020-05-13 …
当a=负的1/2+根号5时,化简9-6a+a^2/a-3加(根号下a^2-2a+1)/a^2-a 2020-05-16 …
高锰酸钾能参与什么反应?这个鬼都知道...我要别的!1他能跟硝酸银生成什么? 2020-06-14 …
应用:现有A、B、C三桶油,先把A桶的1/3倒入B桶,再把B桶的1/4倒入C桶,最后把C桶的1/1 2020-06-27 …
(a+1)的-1/3次方小于(2-a)的-1/3次方A范围第二道和第一道一样后面是(3-2a)的- 2020-07-14 …
一道数学难题已知:a的2/3次方+b的2/3次方=4,x=a+3a的1/3*b的2/3次方,y=b 2020-07-15 …
(a+b)的1到9次方都写出来(a-b)的1到9次方都写出来就直接写出来 2020-07-21 …