早教吧作业答案频道 -->数学-->
如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=22,点E在线段A1D上.(Ⅰ)证明:AA1⊥平面ABCD;(Ⅱ)当A1EED为何值时,A1B∥平面EAC,并求出此时三棱锥E-ACD的
题目详情
如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=2
,点E在线段A1D上.
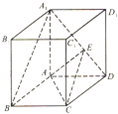
(Ⅰ)证明:AA1⊥平面ABCD;
(Ⅱ)当
为何值时,A1B∥平面EAC,并求出此时三棱锥E-ACD的体积.
| 2 |

(Ⅰ)证明:AA1⊥平面ABCD;
(Ⅱ)当
| A1E |
| ED |
▼优质解答
答案和解析
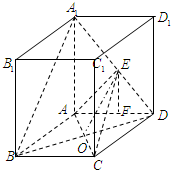 (Ⅰ)∵底面ABCD是菱形,∠ABC=60°,∴AB=AD=AC=2,
(Ⅰ)∵底面ABCD是菱形,∠ABC=60°,∴AB=AD=AC=2,
∵AA1=2,∴AA12+AB2=A1B2,∴AA1⊥AB.
同理,AA1⊥AD,又∵AB⊂平面ABCD,AD⊂平面ABCD,AB∩AD=A.
∴AA1⊥平面ABCD.
(Ⅱ)当E为A1D的中点时,A1B∥平面EAC.
证明:连接BD交AC于O,连接OE,则OE∥A1B,
∴A1B∥平面EAC,此时
=
=1.
∴设AD的中点为F,连接EF,则EF∥AA1,∴EF⊥平面ACD,且EF=1.
∴三棱锥E-ACD的体积VE-ACD=
×1×
×2×2×
=
.
 (Ⅰ)∵底面ABCD是菱形,∠ABC=60°,∴AB=AD=AC=2,
(Ⅰ)∵底面ABCD是菱形,∠ABC=60°,∴AB=AD=AC=2,∵AA1=2,∴AA12+AB2=A1B2,∴AA1⊥AB.
同理,AA1⊥AD,又∵AB⊂平面ABCD,AD⊂平面ABCD,AB∩AD=A.
∴AA1⊥平面ABCD.
(Ⅱ)当E为A1D的中点时,A1B∥平面EAC.
证明:连接BD交AC于O,连接OE,则OE∥A1B,
∴A1B∥平面EAC,此时
| A1E |
| ED |
| BO |
| OD |
∴设AD的中点为F,连接EF,则EF∥AA1,∴EF⊥平面ACD,且EF=1.
∴三棱锥E-ACD的体积VE-ACD=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
看了 如图,四棱柱ABCD-A1B...的网友还看了以下:
(2004•上海)如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上 2020-05-13 …
下列各题中,相关联的两种量成正比例关系的是()A.等边三角形的周长和任意一边的长度B.圆锥的体积一 2020-05-14 …
从(dx)/(dy)=1/y '导出:(d^2x)/(dy^2)=-y''/(y')^3rt另外, 2020-05-17 …
用价层电子对互斥理论预测CO32-和BF3的立体结构分别是()A.平面三角形;三角锥形B.三角锥形 2020-06-22 …
圆锥面的压强计算公式一个圆锥上底直径d下底直径D长L(D>d\)在下底上面加一个F的力,求在圆锥表 2020-06-27 …
v柱:v锥=3:7,d锥:d柱=5:3,h柱:h锥=()列示 2020-07-05 …
求圆锥体的斜度和锥度答案已知一圆锥体,D=24mm,d=22mm,L=32mm,求它的斜度和锥度! 2020-07-05 …
有一个圆锥,高D米,底面积S平方米,现在把高平均分成两份,每份高二分之一米,求下面圆台的体积.(也 2020-07-31 …
人造雨向圆锥瓶内注入少量的温水,稍后取一干燥的蒸发皿盖在瓶口,在蒸发皿中放置一些冰块.观察思考:(1 2020-11-17 …
求圆锥体的斜度和锥度答案已知一圆锥体,D=24mm,d=22mm,L=32mm,求它的斜度和锥度! 2020-12-20 …