早教吧作业答案频道 -->数学-->
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.(1)证明:SO⊥BD;(2)求三棱锥O-SCD的体积.
题目详情
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.
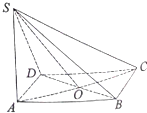
(1)证明:SO⊥BD;
(2)求三棱锥O-SCD的体积.

(1)证明:SO⊥BD;
(2)求三棱锥O-SCD的体积.
▼优质解答
答案和解析
证明:(1)∵SA⊥平面ABCD,BD⊂平面ABCD,
∴SA⊥BD,
∵四边形ABCD是正方形,
∴BD⊥AC,
又SA⊂平面SAC,AC⊂平面SAC,SA∩AC=A,
∴BD⊥平面SAC,∵SO⊂平面SAC,
∴SO⊥BD.
(2)∵四边形ABCD是边长为1的正方形,
∴S△OCD=
S正方形ABCD=
×12=
.
∴VO-SCD=VS-OCD=
S△OCD•SA=
×
×4=
.
∴SA⊥BD,
∵四边形ABCD是正方形,
∴BD⊥AC,
又SA⊂平面SAC,AC⊂平面SAC,SA∩AC=A,
∴BD⊥平面SAC,∵SO⊂平面SAC,
∴SO⊥BD.
(2)∵四边形ABCD是边长为1的正方形,
∴S△OCD=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴VO-SCD=VS-OCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
看了 如图,在四棱锥S-ABCD中...的网友还看了以下:
在长方形ABCD中,O为直角坐标原点,点A为(4,0),点B为(4,6),点c为(0,6)若过点C 2020-05-20 …
对包含n个元素的散列表进行检索,平均检索长度( )。A.为O(log2n)B.为O(n)C.为O(n 2020-05-23 …
对包含n个元素的散列表进行检索,平均检索长度________。A.为O(log2n)B.为O(n)C 2020-05-23 …
对包含n个元素的散列表进行检索,平均检索长度A.为O(10g2n)B.为O(n)C.为O(nlog2 2020-05-23 …
单词辨音,判断每组单词划线部分的读音是(S)否(D)相同1.milk(划线部分为i)this(划线 2020-05-24 …
对包含n个元素的散列表进行检索,平均检索长度A.为O(log2n)B.为O(n)C.为O(n*log 2020-05-24 …
对包含n个元素的散列表进行检索,平均检索长度为A.为O(log2n)B.为O(n)C.为O(n*lo 2020-05-24 …
对包含n个元素的散列表进行检索,平均检索长度A.为O(log2n)B.为O(n)C.为O(nlog2 2020-05-24 …
如图所示,O为地球球心,A为地球表面上的点,B为O、A连线间的点,AB=d,将地球视为质量分布均匀 2020-06-12 …
如图,已知直线l与O相离,OA⊥l于点A,OA与O相交于点P,点B为O上一点,BP的延长线交直线l 2020-07-26 …