早教吧作业答案频道 -->数学-->
如图,△ABC中,AB=AC=8,BC=12,点P、Q分别在AB、BC边上,且∠AQP=∠B.(1)求证:△BQP∽△CAQ;(2)若BP=4.5,求∠BPQ的度数;(3)若在BC边上存在两个点Q,满足∠AQP=∠B,求BP长的取值范围.
题目详情
如图,△ABC中,AB=AC=8,BC=12,点P、Q分别在AB、BC边上,且∠AQP=∠B.
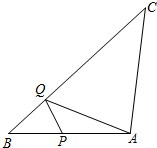
(1)求证:△BQP∽△CAQ;
(2)若BP=4.5,求∠BPQ的度数;
(3)若在BC边上存在两个点Q,满足∠AQP=∠B,求BP长的取值范围.

(1)求证:△BQP∽△CAQ;
(2)若BP=4.5,求∠BPQ的度数;
(3)若在BC边上存在两个点Q,满足∠AQP=∠B,求BP长的取值范围.
▼优质解答
答案和解析
(1)∵AB=AC,
∴∠B=∠C.
∵∠AQP=∠B.
∴∠AQP=∠C.
又∵∠AQB=∠AQP+∠PQB,∠AQB=∠CAQ+∠C,
∴∠PQB=∠CAQ.
∴△BQP∽△CAQ.
(2)∵△BQP∽△CAQ,
∴
=
.
∴
=
,
解得BQ=6.
∵BC=12,
∴BQ=CQ=6.
又∵AB=AC,
∴AQ⊥BC,
∴∠CQA=90°.
∵△BQP∽△CAQ,
∴∠BPQ=∠CQA=90°.
(3)∵△BQP∽△CAQ,
∴
=
.
设BQ=x,BP=m,则
=
,
整理得 x2-12x+8m=0.
∵在BC边上存在两个点Q,
∴方程有两个不相等的正实数根,
∴△=122-32m>0,解得 m<
,
∴BP长的取值范围为0<BP<
.
∴∠B=∠C.
∵∠AQP=∠B.
∴∠AQP=∠C.
又∵∠AQB=∠AQP+∠PQB,∠AQB=∠CAQ+∠C,
∴∠PQB=∠CAQ.
∴△BQP∽△CAQ.
(2)∵△BQP∽△CAQ,
∴
| BQ |
| AC |
| BP |
| CQ |
∴
| BQ |
| 8 |
| 4.5 |
| 12-BQ |
解得BQ=6.
∵BC=12,
∴BQ=CQ=6.
又∵AB=AC,
∴AQ⊥BC,
∴∠CQA=90°.
∵△BQP∽△CAQ,
∴∠BPQ=∠CQA=90°.
(3)∵△BQP∽△CAQ,
∴
| BQ |
| AC |
| BP |
| CQ |
设BQ=x,BP=m,则
| x |
| 8 |
| m |
| 12-x |
整理得 x2-12x+8m=0.
∵在BC边上存在两个点Q,
∴方程有两个不相等的正实数根,
∴△=122-32m>0,解得 m<
| 9 |
| 2 |
∴BP长的取值范围为0<BP<
| 9 |
| 2 |
看了 如图,△ABC中,AB=AC...的网友还看了以下:
指出下列各组条件与结论中,条件p是结论q的什么条件.(1) p:a>2,b>3,q:a+b>5;( 2020-05-14 …
等比数列an=a1*q^(n-1),Sn=a1(1-q^n)/(1-q)∴a3=2=a1*q^(3 2020-05-17 …
指出下列各组条件中,条件p是结论q的什么条件(1)p:ab>o,q:/a/>/b/(4)p:整数a 2020-06-12 …
等比数列an=a1*q^(n-1),Sn=a1(1-q^n)/(1-q)∴a3=2=a1*q^(3 2020-06-17 …
如果(x+q)(x+1/5)的积中不含x项,则q等于(x+q)(x+1/5)=x^2+(q+1/5 2020-07-11 …
把下列各式化成(a-b)^p的形式Ⅰ15(a-b)³[-6(a-b)^(q+5)](b-a)²是不 2020-07-18 …
指出下列各组条件中,条件p是结论q的什么条件(1)p:ab>o,q:/a/>/b/(4)p:整数a 2020-07-30 …
1.若n为整数,a^2n=2,求(2a^3n)^2-3(a^2)^2n.2.若x^p-2-(q-2 2020-07-31 …
如果方程x^2+px+q=0的两个根是x1、x2,那么x1+x2=-p,x1.x2=q,请根据以上结 2020-11-01 …
如图5所示,带有长方体盒子的斜劈A放在固定的斜面体C的斜面上,在盒子内放有光滑球B,B恰与盒子前、后 2020-11-01 …