早教吧作业答案频道 -->数学-->
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界
题目详情
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.
例如:下面所表示的函数的界高为4.
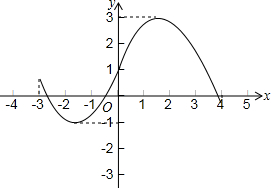
(1)若函数y=kx+1(-2≤x≤1)的界高为4,求k的值;
(2)已知m>-2,若函数y=x2(-2≤x≤m)的界高为4,求实数m的取值范围;
(3)已知a>0,函数y=x2-2ax+3a(-2≤x≤1)的界高为
,求a的值.
例如:下面所表示的函数的界高为4.
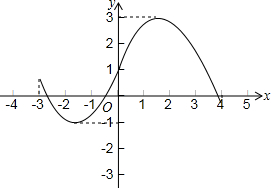
(1)若函数y=kx+1(-2≤x≤1)的界高为4,求k的值;
(2)已知m>-2,若函数y=x2(-2≤x≤m)的界高为4,求实数m的取值范围;
(3)已知a>0,函数y=x2-2ax+3a(-2≤x≤1)的界高为
| 25 |
| 4 |
▼优质解答
答案和解析
(1)将x1=-2代入得;y1=-2k+1,将x2=1代入得:y2=k+1,
∵|y1-y2|=4,
∴|-3k|=4.
解得:k=±
.
(2)将y=4代入抛物线的解析式得:x2=4,解得:x1=-2,x2=2,
∴m=2.
∴m的取值范围是0≤m<2.
(3)当a≥1时,将x1=-2,x2=1代入函数解析式求得y1=4+7a,y2=1+a,
∵|y1-y2|=
,
∴3+6a=
,
解得:a=
又∵a≥1
故此种情况不成立;
当0≤a≤1时,将x1=-2,x2=a代入函数解析式得:y1=4+7a,y2=3a-a2,
∵y1-y2=
,
∴a2+4a-
=0,
解得:a1=
,a2=-
(舍去)
故a=
.
∵|y1-y2|=4,
∴|-3k|=4.
解得:k=±
| 4 |
| 3 |
(2)将y=4代入抛物线的解析式得:x2=4,解得:x1=-2,x2=2,
∴m=2.
∴m的取值范围是0≤m<2.
(3)当a≥1时,将x1=-2,x2=1代入函数解析式求得y1=4+7a,y2=1+a,
∵|y1-y2|=
| 25 |
| 4 |
∴3+6a=
| 25 |
| 4 |
解得:a=
| 13 |
| 24 |
又∵a≥1
故此种情况不成立;
当0≤a≤1时,将x1=-2,x2=a代入函数解析式得:y1=4+7a,y2=3a-a2,
∵y1-y2=
| 25 |
| 4 |
∴a2+4a-
| 9 |
| 4 |
解得:a1=
| 1 |
| 2 |
| 9 |
| 2 |
故a=
| 1 |
| 2 |
看了 若y是关于x的函数,H是常数...的网友还看了以下:
△ABC中,∠ABC=45°,CD垂直AB于D,BD平分∠ABC,且BE⊥AC于E,与CD相交于点F 2020-03-31 …
点P在曲线C x²/4+y²=1上,若若存在过P的直线交曲线C于A点,交直线l:x=4于B点,(长 2020-05-13 …
已知三角形的面积为2.5,一条边为a,这条边上的高为h.反比例关系为h=2.5/a,图像在第一象限 2020-05-13 …
如图,已知平行四边形ABCD,点P在对角线BD上,EF‖BC,GH‖AB,点E,H,F,G分别是在 2020-05-15 …
△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,BE⊥AC于E于CD交于点F,H是 2020-05-20 …
有人建议把H元素排在元素周期表的7主族.下列事实能支持这观点的是1.H原子得到一个电子就可以达到稳 2020-05-24 …
求一数学几何证明题、今天二测的.三角形ABC,角C为钝角,点E、H是边AB上的点,点K和M分别是边 2020-06-03 …
已知等边△abc,它的高为h如图(1)若点p在△abc内,则点p到△abc的三边的距离和h的大小关 2020-06-12 …
已知,M是等边△ABC边BC上的点.(1)如图1,过点M作MN∥AC且交于点N,求证:BM=BN; 2020-06-18 …
在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线 2020-06-19 …