如图一块长方形区域ABCD，AD=2，AB=1，在边AD的中点O处有一个可转动的探照灯，其照射角∠EOF始终为π4，设∠AOE=α，探照灯照射在长方形ABCD内部区域的面积为S；（1）当0≤α<π2时，求S关于

Question

如图一块长方形区域ABCD，AD=2，AB=1，在边AD的中点O处有一个可转动
的探照灯，其照射角∠EOF始终为(π)/(4)，设∠AOE=α，探照灯照射在长方形ABCD内部区域的面积为S；

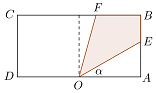
（1）当0≤α<(π)/(2)时，求S关于α的函数关系式；
（2）当0≤α≤(π)/(4)时，求S的最大值；
（3）若探照灯每9分钟旋转“一个来回”（OE自OA转到OC，再回到OA，称“一个来
回”，忽略OE在OA及OC处所用的时间），且转动的角速度大小一定，设AB边上有一点G，且∠AOG=(π)/(6)，求点G在“一个来回”中被照到的时间．

Answer 1

（1）过O作OH⊥BC，H为垂足
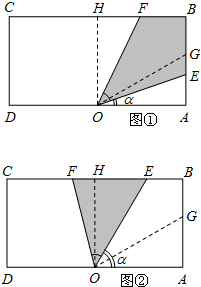
当0≤α≤(π)/(4)，E在边AB上，F在线段BH上（如图①），
此时，AE=tanα，FH=tan（(π)/(4)-α），∴S=S_{正方形OABH}-S_△OAE-S_△OHF
S=1-(1)/(2)tanα-(1)/(2)tan((π)/(4)-α)；
当(π)/(4)<α<(π)/(2)，E在线段BH上，F在线段CH上（如图②），EH=(1)/(tanα)，FH=(1)/(tan((3π)/(4)-α))
S=(1)/(2)((1)/(tanα)+(1)/(tan((3π)/(4)-α)))；

（2）当0≤α≤(π)/(4)，S=1-(1)/(2)tanα-(1)/(2)tan((π)/(4)-α)；
即S=2-(1)/(2)(1+tanα+(2)/(1+tanα))，∴0≤tanα≤1．即1≤1+tanα≤2．
1+tanα+(2)/(1+tanα)≥2√(2)，当tanα=-1时，S取得最大值为2-√(2)
（3）在“一个来回”中，OE共转了2×(3π)/(4)=(3π)/(2)，其中点G被照到时，共转了2×(π)/(6)=(π)/(3)，
∴在“一个来回”中，点G被照到的时间为9×((π)/(3)÷(3π)/(2))=2分钟；