早教吧作业答案频道 -->数学-->
如图,在△ABC中,已知CA=CB=5,BA=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B.(1)求证:∠AEF=∠BCE;(2
题目详情
如图,在△ABC中,已知CA=CB=5,BA=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B.
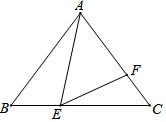
(1)求证:∠AEF=∠BCE;
(2)当以点C为圆心,以CF为半径的圆与AB相切时,求BE的长;
(3)探究:在点E、F的运动过程中,△CEF可能为等腰三角形吗?若能,求出BE的长;若不能,请说明理由.

(1)求证:∠AEF=∠BCE;
(2)当以点C为圆心,以CF为半径的圆与AB相切时,求BE的长;
(3)探究:在点E、F的运动过程中,△CEF可能为等腰三角形吗?若能,求出BE的长;若不能,请说明理由.
▼优质解答
答案和解析
 (1)证明:∵∠B+∠BCE=∠CEA=∠CEF+∠FEA,
(1)证明:∵∠B+∠BCE=∠CEA=∠CEF+∠FEA,
∵∠CEF=∠B,
∴∠AEF=∠BCE;
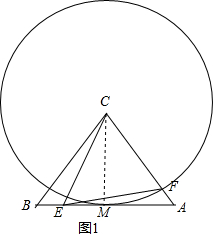
(2) 如图1,设 C与BA切于点M,则CM=CF,CM⊥BA,
∵CA=CB,CM⊥BA∴BM=AM=
=3,
Rt△AMC中,AC=5,AM=3,
∴CF=CM=4,
∴AF=1,
∵CA=CB∴∠B=∠C
由(1)知∠AEF=∠BCE
∴△AEF∽△BCE,
∴
=
,
设BE长为x,则EA长为6-x
∴
=
,
解得:x1=1,x2=5,
答:BE的长为1或5;
(3)可能.如图2,
①当CE=CF时,∠3=∠2=∠A,
∴EF∥AB,此时E与B重合,与条件矛盾,不成立.
②当CF=EF时,
又∵△AEF∽△BCE,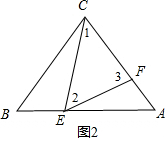
∴△AEF≌△BCE,
∴AE=BC=5,
∴BE=AB-5=1,
③当CF=EF时,∠1=∠2=∠A=∠B,
△FCE∽△CBA,
∴
=
,
∴
=
=
,
∵△AEF∽△BCE
∴
=
=
∴EA=
BC=
×5=
,
∴EB=AB-
=
.
答:当BE的长为1或
时,△CFE为等腰三角形.
 (1)证明:∵∠B+∠BCE=∠CEA=∠CEF+∠FEA,
(1)证明:∵∠B+∠BCE=∠CEA=∠CEF+∠FEA,∵∠CEF=∠B,
∴∠AEF=∠BCE;
(2) 如图1,设 C与BA切于点M,则CM=CF,CM⊥BA,
∵CA=CB,CM⊥BA∴BM=AM=
| AB |
| 2 |
Rt△AMC中,AC=5,AM=3,
∴CF=CM=4,
∴AF=1,
∵CA=CB∴∠B=∠C
由(1)知∠AEF=∠BCE
∴△AEF∽△BCE,
∴
| EA |
| BC |
| AF |
| BE |
设BE长为x,则EA长为6-x
∴
| 6-x |
| 5 |
| 1 |
| x |
解得:x1=1,x2=5,
答:BE的长为1或5;
(3)可能.如图2,
①当CE=CF时,∠3=∠2=∠A,
∴EF∥AB,此时E与B重合,与条件矛盾,不成立.
②当CF=EF时,
又∵△AEF∽△BCE,

∴△AEF≌△BCE,
∴AE=BC=5,
∴BE=AB-5=1,
③当CF=EF时,∠1=∠2=∠A=∠B,
△FCE∽△CBA,
∴
| EF |
| AC |
| CE |
| AB |
∴
| EF |
| CE |
| AC |
| AB |
| 5 |
| 6 |
∵△AEF∽△BCE
∴
| EA |
| BC |
| EF |
| CE |
| 5 |
| 6 |
∴EA=
| 5 |
| 6 |
| 5 |
| 6 |
| 25 |
| 6 |
∴EB=AB-
| 25 |
| 6 |
| 11 |
| 6 |
答:当BE的长为1或
| 11 |
| 6 |
看了 如图,在△ABC中,已知CA...的网友还看了以下:
(1)已知A(0,2),|AB|=6,B点和A点在同一条坐标轴上,求B点的坐标.(2)已知A(0, 2020-04-25 …
一道关于数轴的题,回答对的还可以加分(1)若A点表示数-6,B点表示数8,则线段AB中点所表示的数 2020-04-26 …
如图,在梯形ABCD中,AD平行于BC,∠B=90°,BC=6,AD=3,∠DCB=30°,点E, 2020-05-16 …
已知任意三角型abc,过a点做垂线到bc命点e,过b点做垂线到ac命为f,过c点做垂线到ab命点d 2020-05-20 …
-10<M<0,在M点与原点O之间有6个点A,B,C,D,E,F,这6个点是MO的7等分点,M有几 2020-05-21 …
如图,矩形ABCD中,AB=4,BC=3,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动 2020-07-10 …
在平面直角坐标系中,点O为坐标原点,直线y=2x+6与x轴交于点A,与y轴交于点C,点B为X轴负半 2020-08-02 …
(2013•宜昌)如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1), 2020-11-12 …
一点在另一点什么方向一条纬线上的两点只有东西之分,具体,由于地球是圆的,那么一点究竟是在另一个同一纬 2020-12-01 …
质量为m,电量为q的小球以速度为v0从A点竖直向上进入水平向右的匀强电场E.到B点时的速度大小仍为V 2020-12-15 …