如图，在平面直角坐标系中，抛物线y=-x2+2x+3与x轴交于A，B两点（点A在点B左侧），与y轴交于C点．动点P从点B出发，沿x轴负方向以每秒1个单位的速度运动．过点P作PQ⊥BC，垂足为Q，再将△PBQ

Question

如图，在平面直角坐标系中，抛物线y=-x²+2x+3与x轴交于A，B两点（点A在点B左侧），与y轴交于C点．动点P从点B出发，沿x轴负方向以每秒1个单位的速度运动．过点P作PQ⊥BC，垂足为Q，再将△PBQ绕点P按逆时针方向旋转90°．设点P的运动时间为t秒．

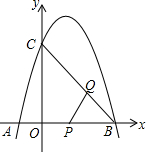
（1）若旋转后的点B落在该抛物线上，则t的值为___．
（2）若旋转后的△PBQ与该抛物线有两个公共点，则t的取值范围是___．

Answer 1

y=-x²+2x+3，当x=0时，解得：y=3，所以OC=3；
当y=0时，0=-x²+2x+3，解得：x₁=-1，x₂=3，所以：OA=1，OB=3，
所以：A（-1，0），B（3，0），C（0，3）
∵OC=OB=3，可知：∠OBC=45°
∵PQ⊥BC，
∴△PBQ是等腰直角三角形，PQ=PB，
运动t秒后，PB=t，运用勾股定理可求BQ=PQ=(√(2))/(2)t，将△PBQ绕点P按逆时针方向旋转90°后，PB⊥x轴，过点Q作QM⊥x轴，垂足为M，可求∠QPM=45°，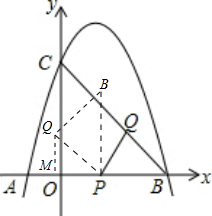
由勾股定理可求：PM=QM=(1)/(2)t，
所以P（3-t，0），Q（3-(3t)/(2)，(t)/(2)），点B（3-t，t），
（1）把点B（3-t，t）坐标代入y=-x²+2x+3得：t=-（3-t）²+2（3-t）+3，解得：t=3，或t=0（舍去）
所以：t=3．
故答案为：3
（2）若PB与抛物线y=-x²+2x+3有交点，由于点B（3-t，t），则有：当x=3-t时，y<t，且3-t<-1，代入得：-（3-t）²+2（3-t）+3≤t，
解得：4>t≥3，或t≤0（舍去）
若PQ，BQ与抛物线y=-x²+2x+3有两个不同交点，由于Q（3-(3t)/(2)，(t)/(2)），则有；当x=3-(3t)/(2)时，y<(t)/(2)，且3-t<-1，代入得：：-（3-(3t)/(2)）²+2（3-(3t)/(2)）+3≤(t)/(2)，
解得：4>t>(22)/(9)，或t≤0（舍去）
所以：当4>t≥3时，PB与PQ与抛物线有交点；当3≥t>(22)/(9)时，PQ和BQ与抛物线有交点，
综上所述：
若旋转后的△PBQ与该抛物线有两个公共点，则t的取值范围是：4>t>(22)/(9)
故答案为：4>t>(22)/(9)