早教吧作业答案频道 -->数学-->
将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:(x2+x+1)0=1(x2+x+1)1=x2+x+1(x2+x+1)2=x4+2x3+3x2+2x+1(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1…观察多项式系数之间的关系,可以仿照杨辉三
题目详情
将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:
(x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
…
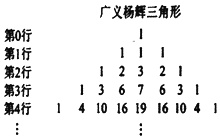
观察多项式系数之间的关系,可以仿照杨辉三角构造如图所示的广义杨辉三角形,其构造方法为:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(1+ax)(x2+x+1)5的展开式中,x8项的系数为67,则实数a值为___.
(x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
…
观察多项式系数之间的关系,可以仿照杨辉三角构造如图所示的广义杨辉三角形,其构造方法为:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(1+ax)(x2+x+1)5的展开式中,x8项的系数为67,则实数a值为___.

▼优质解答
答案和解析
由题意可得广义杨辉三角形第5行为1,5,15,30,45,51,45,30,15,5,1,
所以(1+ax)(x2+x+1)5的展开式中,x8项的系数为15+30a=67,
所以a=
.
故答案为:
.
所以(1+ax)(x2+x+1)5的展开式中,x8项的系数为15+30a=67,
所以a=
| 26 |
| 15 |
故答案为:
| 26 |
| 15 |
看了 将三项式(x2+x+1)n展...的网友还看了以下:
(2014•镇江二模)下列有关说法正确的是()A.常温下,0.1mol•L-1Na2S溶液中存在: 2020-05-14 …
初三数学题关于二次根式设一元二次方程ax²+bx+c=0的两根为x1,x2,则两根与方程系数之间有 2020-05-16 …
快速操动开关产品的分合闸时间为( )。 A.0.05s以下B.0.1s以下C.0.5s以下D.0.5 2020-06-07 …
快速操动开关产品的分合闸时间为( )。 A.0.05s以下 B.0.1s以下 C.0.5s以下D.0 2020-06-07 …
要交今天终于急果子成熟后,从树上落到地面,他落下的高度与经过的时间有如下关系,时间t/秒0.50. 2020-06-11 …
关于向量标架的一道问题已知向量a,b,c的坐标如下:1、在标架{O;e1,e2}下,a={0,1} 2020-06-18 …
常温下Ca(OH)2的溶解度为0.148g,其溶于水达饱和时存在如下关系:常温下Ca(OH)2的溶 2020-07-18 …
问关于定积分的问题若∫(上限π,下限0)xf(sinx)dx=∫(上限π,下限0)(π-t)f(s 2020-07-23 …
关于简单有理式积分的问题:定积分:∫(上限4,下限0) (1+x)√(4x-x^2)d关于简单有理 2020-07-31 …
若一元二次方程ax2+bx+c=0(a≠0)的两个实根为x1、x2,则两根与方程系数之间有如下关系: 2020-11-06 …