早教吧作业答案频道 -->数学-->
已知关于x的方程kx2+(2k+1)x+2=0.(1)求证:无论k取任何实数时,方程总有实数根;(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1
题目详情
已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
▼优质解答
答案和解析
(1)证明:①当k=0时,方程为x+2=0,所以x=-2,方程有实数根,
②当k≠0时,∵△=(2k+1)2-4k×2=(2k-1)2≥0,即△≥0,
∴无论k取任何实数时,方程总有实数根;
(2) 令y=0,则kx2+(2k+1)x+2=0,
解关于x的一元二次方程,得x1=-2,x2=-
,
∵二次函数的图象与x轴两个交点的横坐标均为整数,且k为正整数,
∴k=1.
∴该抛物线解析式为y=x2+3x+2,
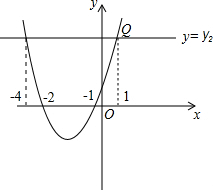
由图象得到:当y1>y2时,a>1或a<-4.
(3)依题意得kx2+(2k+1)x+2-y=0恒成立,即k(x2+2x)+x-y+2=0恒成立,
则
,
解得
或
.
所以该抛物线恒过定点(0,2)、(-2,0).
②当k≠0时,∵△=(2k+1)2-4k×2=(2k-1)2≥0,即△≥0,
∴无论k取任何实数时,方程总有实数根;
(2) 令y=0,则kx2+(2k+1)x+2=0,
解关于x的一元二次方程,得x1=-2,x2=-
| 1 |
| k |
∵二次函数的图象与x轴两个交点的横坐标均为整数,且k为正整数,
∴k=1.
∴该抛物线解析式为y=x2+3x+2,

由图象得到:当y1>y2时,a>1或a<-4.
(3)依题意得kx2+(2k+1)x+2-y=0恒成立,即k(x2+2x)+x-y+2=0恒成立,
则
|
解得
|
|
所以该抛物线恒过定点(0,2)、(-2,0).
看了 已知关于x的方程kx2+(2...的网友还看了以下:
按要求写词。1.描写天气的词语:2.描写春天的词语:3.含有数字的词 2020-04-08 …
关于x的整系数一元二次方程ax2-bx+c=0(a≠0)中,若a+b是偶数,c是奇数,则()A.方 2020-04-09 …
关于线代的问题.晕了,速32.非齐次线性方程组AX=b中未知数的个数为n,方程个数为m,系数矩阵A 2020-05-14 …
对于数列{an},如果对任意正整数n,总有不等式:an+an+22≤an+1成立,则称数列{an} 2020-06-11 …
关于x的一元二次方程kx2-(2k-2)x+(k-2)=0(k≠0).(1)求证:无论k取何值时, 2020-06-12 …
神舟十号总设计师张柏楠说:载人航天工程有数万个节点,几十万条程序语言。相关人员、各个单位都必须密切 2020-06-18 …
神舟十号总设计师张柏楠说过,载人航天工程有数万个节点,几十万条程序语言,相关人员、各个单位都必须密 2020-06-18 …
非齐次线性方程组Ax=b中未知数的个数为n,方程个数为m,系数矩阵A的秩为r,则()A.r=m时, 2020-06-30 …
按下面规则扩充新数:已有两数a、b,可按规则c=ab+a+b扩充一个新数,在a、b、c三个数中任取 2020-06-30 …
已知关于x的方程(m-2)x2-2(m-1)x+m+1=0.当m为何非负整数时.(1)方程只有一个 2020-07-12 …