早教吧作业答案频道 -->数学-->
如图,已知抛物线y=x2-2tx+t2-2的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线与点P.(1)若点C的横坐标为1,且是线段AB的中
题目详情
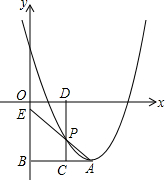
如图,已知抛物线y=x2-2tx+t2-2的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线与点P.
(1)若点C的横坐标为1,且是线段AB的中点,求点P的坐标;
(2)若直线AP交y轴负半轴于点E,且AC=CP,求四边形OEPD的面积S关于t的函数解析式,并写出定义域;
(3)在(2)的条件下,当△ADE的面积等于2S时,求t的值.

(1)若点C的横坐标为1,且是线段AB的中点,求点P的坐标;
(2)若直线AP交y轴负半轴于点E,且AC=CP,求四边形OEPD的面积S关于t的函数解析式,并写出定义域;
(3)在(2)的条件下,当△ADE的面积等于2S时,求t的值.
▼优质解答
答案和解析
(1)∵抛物线y=x2-2tx+t2-2=(x-t)2-2,
∴顶点A(t,-2),
∵点C的横坐标为1,且是线段AB的中点,
∴
=1,
∴t=2,
∴A(2,-2),
∴抛物线的解析式为y=(x-2)2-2=x2-4x+2,
当x=1时,y=1-4+2=-1,
∴P(1,-1);
(2)当AC=CP时,∠EAB=45°,
∴BE=AB=t,即E(0,-2+t),
∴直线AE的解析式为y=-x+t-2,
由
得P(t-1,-1),
∴S=
OD×(OE+DP)=
(t-1)×(-t+2+1),
∴S=-
t2-2t+
(1<t<2);
(3)∵S△ADE=2S,
∴
PD•t=2(-
t2-2t+
),即
t=t2+4t-3,
解得t=2(舍去)或t=
.
∴顶点A(t,-2),
∵点C的横坐标为1,且是线段AB的中点,
∴
| t |
| 2 |
∴t=2,
∴A(2,-2),
∴抛物线的解析式为y=(x-2)2-2=x2-4x+2,
当x=1时,y=1-4+2=-1,
∴P(1,-1);
(2)当AC=CP时,∠EAB=45°,
∴BE=AB=t,即E(0,-2+t),
∴直线AE的解析式为y=-x+t-2,
由
|
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴S=-
| 1 |
| 2 |
| 3 |
| 2 |
(3)∵S△ADE=2S,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解得t=2(舍去)或t=
| 3 |
| 2 |
看了 如图,已知抛物线y=x2-2...的网友还看了以下:
四叶玫瑰线的二四象限怎么来的?四叶玫瑰线方程为r=sin(2θ),二四象限范围为(π/2,π)和( 2020-04-12 …
关于大学的几个思考题,实验名称是《三相电路研究》1:在三相四线制电路中,中线是不允许接熔断器的,为 2020-04-25 …
(18分)下图是我国某地区图,图中虚线为不同时期种植业分布北界。读图回答问题。(1)(5分)与成都 2020-05-01 …
某人准备设计平行四边形图案,拟以长为4cm,5cm,7cm的三条线段中的两条为边,另一条为对角线画 2020-06-21 …
直四棱柱的两个命题!(1):对角线相等的四棱柱为直四棱柱.为什么对了?((斜的四棱柱对角线不相等吗 2020-07-04 …
如图所示,实线为不知方向的三条电场线,从电场中M点以相同速度飞出a、b两个带电粒子,运动轨迹如图中 2020-07-13 …
空间有6个点,其中任何三点不共线,任何四点不共面,以其中的四点为顶点共可作出个四面体,经过其中每两 2020-07-13 …
(2013•乐山模拟)如图所示,实线为不知方向的三条电场线,从电场中M点以相同速度飞出a、b两个带 2020-07-20 …
已知抛物线的焦点为F,F关于原点的对称点为P.过F做X轴的垂线交抛物线于M,N两点.有下列四个命题 2020-08-01 …
可不可以只用直尺,圆规三等分一直线呢?书上说不可以,我想可以.线段,我认为可以啊,可以先画等距的四 2020-08-02 …