早教吧作业答案频道 -->数学-->
已知函数f(x)=2ax2+3b(a,b∈R),若对于任意x∈[-1,1],都有|f(x)|≤1成立,则ab的最大值是.
题目详情
已知函数f(x)=2ax2+3b(a,b∈R),若对于任意x∈[-1,1],都有|f(x)|≤1成立,则ab的最大值是___.
▼优质解答
答案和解析
函数f(x)=2ax2+3b图象的顶点为(0,3b),
若若对于任意x∈[-1,1],都有|f(x)|≤1成立,
则
,
其对应的平面区域如下图所示:
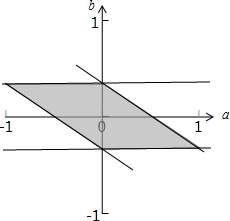
令Z=ab,则在第一,三象限a,b同号时ab取最大值,
由2a+3b=1,a>0,b>0得:ab≤
=
,
故答案为:
若若对于任意x∈[-1,1],都有|f(x)|≤1成立,
则
|
其对应的平面区域如下图所示:

令Z=ab,则在第一,三象限a,b同号时ab取最大值,
由2a+3b=1,a>0,b>0得:ab≤
| (2a+3b)2 |
| 24 |
| 1 |
| 24 |
故答案为:
| 1 |
| 24 |
看了 已知函数f(x)=2ax2+...的网友还看了以下:
已知函数f(x)=2∧x-a╱2∧x+1(a>-1)1.当a=2时,证明f(x)不是奇函数2.判断函 2020-03-31 …
已知函数f(x)=x-1-alnx (a∈R).求证:f(x)≥0恒成立的充要条件是a=1②必要性 2020-05-15 …
已知函数f(x)=(x^2+2x+a)/x,x∈[1,+∞).(1)当a=0.5时,求函数f(x) 2020-05-15 …
设函数f(x)=x2-mlnx,h(x)=x2-x+a(1)当a=0时,f(x)>=h(x)在(1 2020-07-02 …
设函数f(x)和g(x)分别是R上的偶函数和奇函数,则下列结论恒成立的是().设函数f(x)和g( 2020-07-08 …
已知函数f(x)=(x平方+2x+a)/x,x∈[1,正无穷),(1)当a=1/2时,求函数f(已 2020-07-27 …
已知函数f(x)=lnx-a(x-1)/(x>0)(1)讨论函数f(x)的单调性(2)当X大于等于 2020-08-01 …
1.已知函数f(x),如果存在给定的实数对(a,b),使得f(a+x)*f(a-x)=b恒成立,则 2020-08-03 …
给这几个命题的证明,1.若f(x+a)=f(b-x),对于x∈R恒成立,则y=f(x)的图象关于直线 2020-11-11 …
19.对于函数f(x),若存在实数对(a,b),使得等式f(a+x)*f(a-x)=b对定义域中的每 2020-12-08 …