早教吧作业答案频道 -->数学-->
观察下列三角形数表,假设第n行的第二个数为an(n≥2,n∈N),(1)依次写出第六行的所有6个数字;(2)归纳出an+1与an的关系式,并利用递推关系式求出an的通项公式(可以不证明).
题目详情
观察下列三角形数表,假设第n行的第二个数为an(n≥2,n∈N),
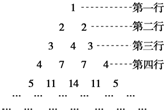
(1)依次写出第六行的所有6个数字;
(2)归纳出an+1与an的关系式,并利用递推关系式求出an的通项公式(可以不证明).

(1)依次写出第六行的所有6个数字;
(2)归纳出an+1与an的关系式,并利用递推关系式求出an的通项公式(可以不证明).
▼优质解答
答案和解析
(1)依据“中间的数从第三行起,每一个数等于它两肩上的数之和”,
得到第六行的所有6个数字分别为:6,16,25,25,16,6.
(2)依题意an+1=an+n(n≥2),a2=2.
所以a3-a2=2,a4-a3=3,…,an-an-1=n-1,
累加得an-a2=2+3+…+(n-1)=
,
则an=
(n2-n+2),
当n=2时a2=
×22-
×2+1=2,也满足上述等式,
所以an=
(n2-n+2)(n≥2,n∈N).
得到第六行的所有6个数字分别为:6,16,25,25,16,6.
(2)依题意an+1=an+n(n≥2),a2=2.
所以a3-a2=2,a4-a3=3,…,an-an-1=n-1,
累加得an-a2=2+3+…+(n-1)=
| (n-2)(n+1) |
| 2 |
则an=
| 1 |
| 2 |
当n=2时a2=
| 1 |
| 2 |
| 1 |
| 2 |
所以an=
| 1 |
| 2 |
看了 观察下列三角形数表,假设第n...的网友还看了以下:
已知Sn=2Sn-1+1,a1=1,求数列的通项公式前n想和Sn因为Sn-Sn-1=an所以Sn= 2020-04-07 …
2011年科学家发现了一种新型火箭推进剂,其化学式为N(NO2)3,下列有关该物质的说法正确的是A 2020-04-08 …
由若干盆花组成的三角形图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案花盆总数是S:n=2 2020-05-13 …
已知弧长和弦长求半径弧长a,弦长b,求半径r,圆心角n?公式12πr*n/360=an=360a/ 2020-05-13 …
裂项公式:1/[n(n+k)]=(1/k)[1/n–1/(n+k)]是咋推出来的啊!望赐教,谢裂项 2020-06-25 …
已知多项式6减2X的二次方减my减12+3y减nx的二次方合并同类项后不含有x、y项,求m+n的值 2020-06-27 …
对于多项式(n-1)xm+2-3x2+2x(其中m是大于-2的整数).(1)若n=2,且该多项式是 2020-07-27 …
已知递推公式An=n*A(n-1)+(n-1)!,求An可以写成其他形式吗?不用阶乘,而用关于n的 2020-08-01 …
请老师写一个大智慧排序公式。N天内涨幅和跌幅排行公式。(要求点击一下是N天的涨幅,再点击一下是N天的 2020-11-27 …
求代数式的值:(1)6+2x²-3x+x²+1,其中x=-5(2)4x²+3xy-x²-9,其中x= 2020-12-31 …