如图所示，两个相同的声源S1和S2相距d=10m，频率f=1700Hz，振动为同步振动，Q是S1，S2连线的中点，OQ是S1，S2连线的中垂线，OQ长l=400m，OP线段平行于S1S2连线，OP=16m，已知空气中声速为340m/s，试

Question

如图所示，两个相同的声源S₁和S₂相距d=10m，频率f=1700Hz，振动为同步振动，Q是S₁，S₂连线的中点，OQ是S₁，S₂连线的中垂线，OQ长l=400m，OP线段平行于S₁S₂连线，OP=16m，已知空气中声速为340m/s，试问：

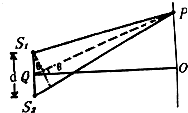
（1）在O点振动将加强还是减弱；
（2）在OP线段上会出现几个振动最强的位置．

Answer 1

（1）由题意可知，根据公式λ=(v)/(f)，则有：λ=(340)/(1700)=0.2m；当到两波源的间距差为波长的整数倍或0时，出现振动加强点，
由于Q是S₁，S₂连线的中点，OQ是S₁，S₂连线的中垂线，所以O点到S₁，S₂的距离是相等的，距离的差是0，所以是振动的加强点．
（2）P到两个波源的距离：

.

PS1

=√(OQ2+(OP-(d)/(2))2)=√(4002+(16-(10)/(2))2)=√(1721)≈41.485m，

.

PS2

=√(OQ2+(OP+(d)/(2))2)=√(4002+(16+(10)/(2))2)=√(2041)≈45.177m
△s=

.

PS2

-

.

PS1

=45.177m-41.485m=3.692m
根据振动的加强点的条件可知，每一次到两个波源的距离的差达到0.2m时就可以出现振动的加强点，所以共有：
n=(△s)/(λ)=(3.692)/(0.2)=18.46
n只能取整数，所以在OP线段上会出现18个振动最强的位置．
答：（1）在O点振动将加强；
（2）在OP线段上会出现18个振动最强的位置．