早教吧作业答案频道 -->数学-->
如图,椭圆E的方程为x2a2+y2b2=1(a>b>0),点O为坐标原点,点A,B分别是椭圆的右顶点和上顶点,点M在线段AB上,满足BM=2MA,直线OM的斜率为14.(1)求椭圆E的离心率e;(2)设点C的坐标
题目详情
如图,椭圆E的方程为
+
=1(a>b>0),点O为坐标原点,点A,B分别是椭圆的右顶点和上顶点,点M在线段AB上,满足BM=2MA,直线OM的斜率为
.
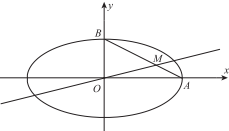
(1)求椭圆E的离心率e;
(2)设点C的坐标为(0,-b),N为线段AC的中点,点N关于直线AB的对称点的纵坐标为
,求椭圆E的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |

(1)求椭圆E的离心率e;
(2)设点C的坐标为(0,-b),N为线段AC的中点,点N关于直线AB的对称点的纵坐标为
| 11 |
| 5 |
▼优质解答
答案和解析
(1)设A(a,0),B(0,b),
∵BM=2MA,由比例性质可得M(
,
),
又∵直线OM的斜率为
,
∴
=
,即
=
,
∴a=2b,a2=4b2=4(a2-c2),则e=
=
;
(2)∵C(0,-b),A(2b,0),
则由中点坐标公式可得N(b,-
),
直线AB:
+
=1,即x+2y-2b=0.
设N关于直线AB的对称点是N′(x0,
),
则
,消去x0得b=2,则a=2b=4.
椭圆方程为:
+
=1.
∵BM=2MA,由比例性质可得M(
| 2a |
| 3 |
| b |
| 3 |
又∵直线OM的斜率为
| 1 |
| 4 |
∴
| ||
|
| 1 |
| 4 |
| 2a |
| 3 |
| 4b |
| 3 |
∴a=2b,a2=4b2=4(a2-c2),则e=
| c |
| a |
| ||
| 2 |
(2)∵C(0,-b),A(2b,0),
则由中点坐标公式可得N(b,-
| b |
| 2 |
直线AB:
| x |
| 2b |
| y |
| b |
设N关于直线AB的对称点是N′(x0,
| 11 |
| 5 |
则
|
椭圆方程为:
| x2 |
| 16 |
| y2 |
| 4 |
看了 如图,椭圆E的方程为x2a2...的网友还看了以下:
设椭圆x2/a2+y2/b2=1的左右顶点分别为A(-2,0),B(2,0).离心率e=√3/2, 2020-05-02 …
如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的右下 2020-05-17 …
如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下 2020-05-17 …
如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下 2020-05-17 …
到达巅顶的经脉是A.足厥阴肝经B.足少阴肾经C.足太阴脾经D.手少阴心经E.手太阴肺经 2020-06-07 …
已知椭圆C:(a>b>0)的离心率e=,点F为椭圆的右焦点,点A,B分别为椭圆长轴的左、右顶点,点 2020-06-21 …
椭圆C:x2a2+y2b2=1(a>b>0)的左、右顶点分别A、B,椭圆过点(0,1)且离心率e= 2020-06-21 …
如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的右下 2020-06-26 …
如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下 2020-07-08 …
如图,椭圆E的方程为x2a2+y2b2=1(a>b>0),点O为坐标原点,点A,B分别是椭圆的右顶 2020-08-02 …