早教吧作业答案频道 -->数学-->
设函数f(x)=lnx+mx,m∈R(1)当m=e(e为自然对数的底数)时,f(x)的极小值;(2)若函数g(x)=f′(x)-x3存在唯一零点,求m的范围.
题目详情
设函数f(x)=lnx+
,m∈R
(1)当m=e(e为自然对数的底数)时,f(x)的极小值;
(2)若函数g(x)=f′(x)-
存在唯一零点,求m的范围.
| m |
| x |
(1)当m=e(e为自然对数的底数)时,f(x)的极小值;
(2)若函数g(x)=f′(x)-
| x |
| 3 |
▼优质解答
答案和解析
解 (1)由题设,当m=e时,f(x)=ln x+
,
则f′(x)=
,由f′(x)=0,得x=e.
∴当x∈(0,e),f′(x)<0,f(x)在(0,e)上单调递减,
当x∈(e,+∞),f′(x)>0,f(x)在(e,+∞)上单调递增,
∴当x=e时,f(x)取得极小值f(e)=ln e+
=2,
∴f(x)的极小值为2…(4分)
(2)由题设g(x)=f′(x)-
=
-
-
(x>0),
令g(x)=0,得m=-
x3+x(x>0).
设φ(x)=-
x3+x(x≥0),
则φ′=-x2+1=-(x-1)(x+1),
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增;
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递减.
∴x=1是φ(x)的唯一极值点,且是极大值点,因此x=1也是φ(x)的最大值点.
∴φ(x)的最大值为φ(1)=
.
又φ(0)=0,结合y=φ(x)的图象(如图),
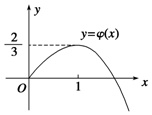
可知
当m=
时,函数g(x)有且只有一个零点;
当m≤0时,函数g(x)有且只有一个零点.
所以,当m=
或m≤0时,函数g(x)有且只有一个零点;…(12分)
| e |
| x |
则f′(x)=
| x-e |
| x2 |
∴当x∈(0,e),f′(x)<0,f(x)在(0,e)上单调递减,
当x∈(e,+∞),f′(x)>0,f(x)在(e,+∞)上单调递增,
∴当x=e时,f(x)取得极小值f(e)=ln e+
| e |
| e |
∴f(x)的极小值为2…(4分)
(2)由题设g(x)=f′(x)-
| x |
| 3 |
| 1 |
| x |
| m |
| x2 |
| x |
| 3 |
令g(x)=0,得m=-
| 1 |
| 3 |
设φ(x)=-
| 1 |
| 3 |
则φ′=-x2+1=-(x-1)(x+1),
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增;
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递减.
∴x=1是φ(x)的唯一极值点,且是极大值点,因此x=1也是φ(x)的最大值点.
∴φ(x)的最大值为φ(1)=
| 2 |
| 3 |
又φ(0)=0,结合y=φ(x)的图象(如图),

可知
当m=
| 2 |
| 3 |
当m≤0时,函数g(x)有且只有一个零点.
所以,当m=
| 2 |
| 3 |
看了 设函数f(x)=lnx+mx...的网友还看了以下:
已知函数f(x)=(1+ln(x+1))/x,g(x)=x-1-ln(x+1)(1)求证:函数y=g 2020-03-30 …
已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)=n-g(x)m+2g(x)是 2020-05-02 …
已知函数,g(x)=log2x,则F(x)=f(x)-g(x)的零点个数是A.4B.3C.2D.1 2020-05-13 …
已知a是不为零的常数,二次函数g(x)=ax^2-x的定义域为R,函数y=g(x-4)为偶函数.函 2020-05-13 …
已知a是不为零的常数,二次函数g(x)=ax2-x的定义域为R,函数y=g(x-4)为偶函数.函数 2020-05-13 …
有关连续性随机变量与概率密度函数的关系请问随机变量的取值为何只在概率密度不为零的区间内取得?随机变 2020-05-16 …
关于函数零点的大小比较f(x)2^x+2,g(x)=x+log(2)X,h(x)=x^3+x的零点 2020-05-17 …
如图,已知A、B、C、D、E、F、G、H、J、K是10个互不相等的非零自然数,并且A=B+C,B= 2020-06-12 …
已知f(x)=3xx≥0f(x)=㏒3(-x)x<0函数:g(x)=f2(x)+f(x)+t,关于 2020-06-13 …
y=f(x)是定义域为R的函数,g(x)=f(x+1)+f(5-x),若函数y=g(x)有且仅有4 2020-06-16 …