早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.(1)求证:点O在∠BAC的平分线上;(2)若AC=5,BC=12,求OE的长.
题目详情
如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
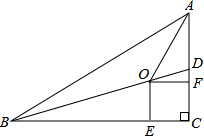
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.

(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
▼优质解答
答案和解析
(1)证明:过点O作OM⊥AB,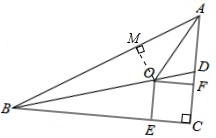
∵BD是∠ABC的一条角平分线,
∴OE=OM,
∵四边形OECF是正方形,
∴OE=OF,
∴OF=OM,
∴AO是∠BAC的角平分线,即点O在∠BAC的平分线上;
(2) ∵在Rt△ABC中,AC=5,BC=12,
∴AB=
=
=13,
设CE=CF=x,BE=BM=y,AM=AF=z,
∴
,
解得:
,
∴CE=2,
∴OE=2.

∵BD是∠ABC的一条角平分线,
∴OE=OM,
∵四边形OECF是正方形,
∴OE=OF,
∴OF=OM,
∴AO是∠BAC的角平分线,即点O在∠BAC的平分线上;
(2) ∵在Rt△ABC中,AC=5,BC=12,
∴AB=
| AC2+BC2 |
| 52+122 |
设CE=CF=x,BE=BM=y,AM=AF=z,
∴
|
解得:
|
∴CE=2,
∴OE=2.
看了 如图,在Rt△ABC中,∠C...的网友还看了以下:
如图 在矩形abcd中 ab=12cm bc=6cm 点P沿AB边从点A开始向点B以2厘米/秒的速 2020-05-16 …
1.点(2,-1)按向量a平移后得(-2,1),它把点(-2,1)平移到()A.(2,-1)B.( 2020-05-23 …
已知矩形ABCD中,AB=10cm,AD=4cm,作如下折叠操作.如图1和图2所示.在边AB上取点 2020-06-08 …
某学生对函数f(x)=2x•cosx的性质进行研究,得出如下的4个结论,其中正确的结论是()A.函 2020-06-10 …
已知:如图,在△ABC中,AB=AC=15,cos∠A=45.点M在AB边上,AM=2MB,点P是 2020-06-12 …
(2013•闸北区一模)已知:如图,在△ABC中,AB=AC=15,cos∠A=45.点M在AB边 2020-07-16 …
(2011•北京模拟)设f(x,y)=x3-4x2+2xy-y2,则下面结论正确的是()A.点(2 2020-07-31 …
在平面直角坐标系中,四边形0ABC是正方形,点A的坐标为(4,0).点P为边AB上一点,∠CPB= 2020-07-31 …
如图,点M是矩形ABCD的边AD的中点.点P是BC边上一动点,PE⊥MC,PF⊥BM.垂足为E、F 2020-08-03 …
(2013•苏州)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x,y 2020-11-12 …