早教吧作业答案频道 -->数学-->
函数的图象关于直线对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是.
题目详情
函数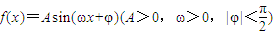 的图象关于直线
的图象关于直线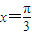 对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 .
对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 .
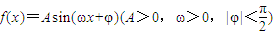 的图象关于直线
的图象关于直线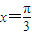 对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 .
对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 . ▼优质解答
答案和解析
【答案】 分析: 先根据函数的最小正周期求出ω的值,因为函数的对称轴为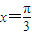 ,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.
,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.
函数f(x)=Asin(ωx+∅)的周期T=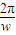 =π,∴ω=2
=π,∴ω=2
∵函数f(x)=Asin(2x+∅)的图象关于直线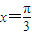 对称,∴f(0)=f(
对称,∴f(0)=f(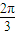 )
)
即Asin∅=Asin(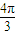 +∅),化简得,sin∅=-
+∅),化简得,sin∅=-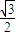 cos∅-
cos∅- sinφ
sinφ
 sin∅=-
sin∅=-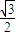 cos∅,tan∅=-
cos∅,tan∅=-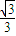 ,
,
又∵|∅|<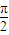 ,∴∅=-
,∴∅=-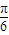 ,∴f(x)=Asin(2x-
,∴f(x)=Asin(2x-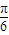 )
)
令2x-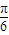 =kπ,k∈Z,解得,x=
=kπ,k∈Z,解得,x=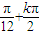 ,k∈Z,
,k∈Z,
∴函数y=f(x)图象的对称中心是(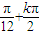 ,0),k∈Z
,0),k∈Z
其中,离坐标原点O最近的对称中心是(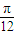 ,0)
,0)
故答案为(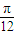 ,0)
,0)
点评: 本题主要考查y=Asin(ωx+∅)的图象与性质,解题时借助基本的正弦函数的图象和性质.
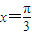 ,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.
,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.函数f(x)=Asin(ωx+∅)的周期T=
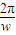 =π,∴ω=2
=π,∴ω=2∵函数f(x)=Asin(2x+∅)的图象关于直线
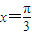 对称,∴f(0)=f(
对称,∴f(0)=f(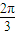 )
)即Asin∅=Asin(
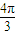 +∅),化简得,sin∅=-
+∅),化简得,sin∅=-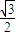 cos∅-
cos∅- sinφ
sinφ sin∅=-
sin∅=-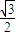 cos∅,tan∅=-
cos∅,tan∅=-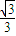 ,
,又∵|∅|<
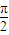 ,∴∅=-
,∴∅=-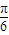 ,∴f(x)=Asin(2x-
,∴f(x)=Asin(2x-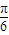 )
)令2x-
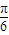 =kπ,k∈Z,解得,x=
=kπ,k∈Z,解得,x=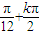 ,k∈Z,
,k∈Z,∴函数y=f(x)图象的对称中心是(
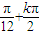 ,0),k∈Z
,0),k∈Z其中,离坐标原点O最近的对称中心是(
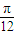 ,0)
,0)故答案为(
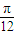 ,0)
,0)点评: 本题主要考查y=Asin(ωx+∅)的图象与性质,解题时借助基本的正弦函数的图象和性质.
看了 函数的图象关于直线对称,它的...的网友还看了以下:
室内有一根直尺,无论怎样放置,在地面上总有这样的直线与直尺所在的直线()答案是垂直,但我认为直尺与地 2020-03-30 …
填空题:两条直线互相垂直,其中一条直线是另一条直线的(),它们的交叉点叫做什么两条直线互相垂直时,其 2020-03-30 …
下列说法正确的有()个①不相交的两条直线是平行线;②两条直线相交所成的四个角中,如果有三个角相等, 2020-04-08 …
“如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线与这个平面垂直”那是这条直线是否要垂直 2020-05-13 …
(1)如果一条直线垂直于一个平面内的三角形的三条边,那么这条直线是否与平面垂直(2)如果一条直线垂 2020-05-13 …
1.如果三条直线共点,且两两垂直,问其中一条直线是否垂直于另两条直线所确定的平面2.已知三角形AB 2020-05-13 …
1下列说法中,正确的是()A和圆的直径垂直的直线一定是圆的切线B经过直径的一端的直线是圆的切线C经 2020-05-21 …
点在直线上,点在直线外要怎么理解这句话啊?点在直线上就是直线是由点组成的而点在直线外根据直线它是向 2020-06-17 …
CAD2012画直线,怎么不能通过直接输入两点的坐标完成直线呢?之前一直用的2008,现在换成20 2020-06-17 …
给出下列说法:(1)与圆只有一个公共点的直线是圆的切线;(2)与圆心的距离等于半径的直线是圆的切线 2020-07-06 …