早教吧作业答案频道 -->数学-->
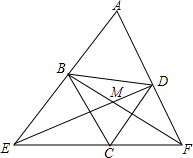
如图,菱形ABCD中∠A=60°,过点C的直线分别交AB、AD的延长线于E、F,BF与DE相交于M.求证:(1)BD是BE和DF的比例中项;(2)BD是DM和DE的比例中项.
题目详情
如图,菱形ABCD中∠A=60°,过点C的直线分别交AB、AD的延长线于E、F,BF与DE相交于M.求证:
(1)BD是BE和DF的比例中项;
(2)BD是DM和DE的比例中项.

(1)BD是BE和DF的比例中项;
(2)BD是DM和DE的比例中项.
▼优质解答
答案和解析
(1)∵ 四边形ABCD是菱形,
四边形ABCD是菱形,
∴AB=AD=BC=CD,AB∥CD,AD∥BC,
∴∠EBC=∠A=∠CDF,∠AEF=∠DCF,
∴△BCE∽△CDF,
∴
=
,
∵∠A=60°,
∴△ABD是等边三角形,
∴BD=BC=CD,
∴
=
,
∴BD2=BE•DF,
即BD是BE和DF的比例中项;
(2)∵
=
,
∵∠EBD=∠BDF=120°,
∴△DBE∽△FBD,
∴∠BED=∠FBD,
∵∠BDM=∠BDE,
∴△BDM∽△EBD,
∴
=
,
∴BD2=DE•DM,
即BD是DM和DE的比例中项.
 四边形ABCD是菱形,
四边形ABCD是菱形,∴AB=AD=BC=CD,AB∥CD,AD∥BC,
∴∠EBC=∠A=∠CDF,∠AEF=∠DCF,
∴△BCE∽△CDF,
∴
| BE |
| CD |
| BC |
| DF |
∵∠A=60°,
∴△ABD是等边三角形,
∴BD=BC=CD,
∴
| BE |
| BD |
| BD |
| DF |
∴BD2=BE•DF,
即BD是BE和DF的比例中项;
(2)∵
| BE |
| BD |
| BD |
| DF |
∵∠EBD=∠BDF=120°,
∴△DBE∽△FBD,
∴∠BED=∠FBD,
∵∠BDM=∠BDE,
∴△BDM∽△EBD,
∴
| BD |
| DE |
| DM |
| BD |
∴BD2=DE•DM,
即BD是DM和DE的比例中项.
看了 如图,菱形ABCD中∠A=6...的网友还看了以下:
1.在三角形ABC中,BD,CE分别是边AC,BA上的中线,M,N分别是BD,CE的中点,若BC=4 2020-03-30 …
从1至10这十个整数中,选出A、B、C、D、E、五个数满足下面六个条件:(1)D比6大;(2)D能 2020-05-13 …
如图,在矩形ABCD中,AB=5,AD=8,直角尺的直角顶点E在AD上滑动时(点E与A,D不重合) 2020-05-16 …
如果两个相似三角形对应高的比为5比4,对应中线的比为?对应叫平分线的比?若三角形ABC与三角形A' 2020-06-02 …
如图,四边形ABCD为菱形,已知A(0,6),D(-8,0).(1)求点C的坐标;(2)设菱形AB 2020-06-03 …
如图m是平行四边形的边AB的中点,CM与BD相交于点E,求三角形与四边形的比A在左下角,B在右下角 2020-07-30 …
如图在四边形ABCD中,角B=∠D=90角a比角c=1比2AB=2CD=1四边形ABCD是一个直角 2020-08-01 …
(2011•广州)如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′, 2020-08-02 …
从1至10十个整数中,选出5个数A,B,C,D,E满足下面6个条件;(1)D比6大;(2)D能被C整 2020-11-20 …
A、B、C、D、E、F、G按比赛结果的名次排列情况如下(其中没有相同名次):1)E得第二名或第三名. 2020-11-24 …