早教吧作业答案频道 -->数学-->
如图，△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，则△DEF与△ABC的面积比是（）A、1：6B、1：5C、1：4D、1：2
题目详情
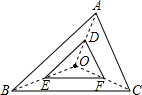如图，△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，则△DEF与△ABC的面积比是（ ）| A、1：6 | B、1：5 |
| C、1：4 | D、1：2 |
▼优质解答
答案和解析
考点：
位似变换
专题：
计算题
分析：
根据两三角形为位似图形，且点O是位似中心，D、E、F分别是OA、OB、OC的中点，求出两三角形的位似比，根据面积之比等于位似比的平方即可求出面积之比．
∵△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，∴两图形的位似之比为1：2，则△DEF与△ABC的面积比是1：4．故选C．
点评：
此题考查了位似变换，位似是相似的特殊形式，位似比等于相似比，其对应的面积比等于相似比的平方．
考点：
位似变换
专题：
计算题
分析：
根据两三角形为位似图形，且点O是位似中心，D、E、F分别是OA、OB、OC的中点，求出两三角形的位似比，根据面积之比等于位似比的平方即可求出面积之比．
∵△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，∴两图形的位似之比为1：2，则△DEF与△ABC的面积比是1：4．故选C．
点评：
此题考查了位似变换，位似是相似的特殊形式，位似比等于相似比，其对应的面积比等于相似比的平方．
看了 如图，△DEF与△ABC是位...的网友还看了以下：
若不等式组x+a≥0 1-2x＞x-2 有解,则a的取值范围是?A.a＞-1 B.a≥-1 C.a 2020-05-15 …
已知多项式x3+ax2+bx+c能被x2+3x-4整除.1）求4a+c的值；（2）求2a-2b-c 2020-05-16 …
不等式a>0c>0ac=1(a²/c²+1)+(c²/a²+1)的最小值不好意思(c¹+1）与（a 2020-06-05 …
符合下列条件的三角形有且只有一个的是（）A.a=1，b=2，c=3B.a=1，b=2，∠A=30° 2020-06-12 …
“已知一次函数的图像进过A(0,-3),B(1,a),C(a,有难度,已知一次函数的图象经过A(0 2020-06-13 …
设有理数a,b,c都不为0,且a+b+c=0,则1/(b²+c²-a²)+1/(c²+a²-b²) 2020-06-14 …
设有理数a、b、c均不为0,且a+b+c=0,求设有理数a、b、c均不为0,且a+b+c=0,求1 2020-06-14 …
已知a,b,c为互不相等的三个数,求证：(1/b-c)^2+(1/c-a)^2+(1/a-b)^2 2020-06-15 …
求救:已知abc三个字母绝对值分别大于1,求证绝对值(a+b+c+a*b*c/1+a*b+b*c+ 2020-06-25 …
若关于x的方程x+2/x=c+2/c的解是x1＝c,x2=2/c,则关于x的方程x+2/(x-1) 2020-06-27 …