在长方体ABCD—A1B1C1D1中AD=4AA1=3问A1B1与BC1是否为异面直线.若是异面直线求出它们之间的距离;若不是异面直线请说明理由.

Question

在长方体ABCD—A ₁ B ₁ C ₁ D ₁ 中 AD=4 AA ₁ =3 问A ₁ B ₁ 与BC ₁ 是否为异面直线.若是异面直线 求出它们之间的距离;若不是异面直线 请说明理由.

Answer 1

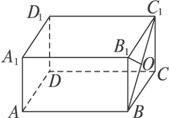
解析:利用异面直线的判定定理判断两条直线是否为异面直线 作出异面直线的公垂线段求其距离.

解:∵点A ₁ 不在平面BB ₁ C ₁ C 内 B ₁ 不在BC ₁ 上

∴A ₁ B ₁ 与BC ₁ 是异面直线.

过B ₁ 作B ₁ O⊥BC ₁ 于O.

由长方体的性质知A ₁ B ₁ 垂直于平面BB ₁ C ₁ C 内的任意一条直线

∴A ₁ B ₁ ⊥B ₁ O.

∴线段B ₁ O是异面直线A ₁ B ₁ 与BC ₁ 的公垂线段.

在△BB ₁ C ₁ 中 BB ₁ =3 B ₁ C ₁ =4 ∠BB ₁ C ₁ =90°.

∴BC ₁ = =5.

∴B ₁ O= .

因此 A ₁ B ₁ 与BC ₁ 是异面直线 它们之间的距离是 .

小结:(1)判断两条直线是否为异面直线常用判定定理:过平面外一点和平面内一点的直线 和平面内不经过该点的直线是异面直线; (2)求异面直线的距离可以作出异面直线的公垂线段 并求其长度.