早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分别为AB,CD的中点,AE的延长线交CB于F.现将△ACD沿CD折起,折成二面角A-CD-B,连接AF.(I)求证:平面AEF⊥平面CBD;(II)当二面角A-CD-B为直二面
题目详情
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分别为AB,CD的中点,AE的延长线交CB于F.现将△ACD沿CD折起,折成二面角A-CD-B,连接AF.
(I)求证:平面AEF⊥平面CBD;
(II)当二面角A-CD-B为直二面角时,求直线AB与平面CBD所成角的正切值.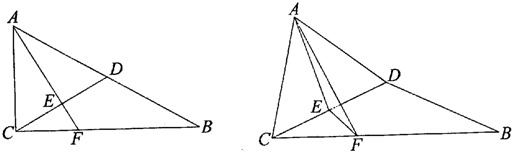
(I)求证:平面AEF⊥平面CBD;
(II)当二面角A-CD-B为直二面角时,求直线AB与平面CBD所成角的正切值.

▼优质解答
答案和解析
 (I)证明:在Rt△ABC中,D为AB的中点,
(I)证明:在Rt△ABC中,D为AB的中点,
得AD=CD=DB,又∠B=30°,得△ACD是正三角形,
又E是CD的中点,得AE⊥CD.(3分)
折起后,AE⊥CD,EF⊥CD,
又AE∩EF=E,AE⊂平面AED,EF⊂平面AEF,
故CD⊥平面AEF,(6分)
又CD⊂平面CDB,
故平面AEF⊥平面CBD.(7分)
(II) ∵二面角A-CD-B是直二面角,
且AE⊥CD,∴AE⊥平面CBD.(8分)
连接EB,AB,则∠ABE就是直线AB与
平面CBD所成的角.(9分)
设AC=a,在△CDB中,
∠DCB=30°,CE=
,CB=
a,
∴EB2=CE2+CB2-2CE•CB•cos∠DCB=
a2,又AE=
a,在Rt△AEB中,tan∠ABE=
=
=
.
∴直线AB与平面CBD所成角的正切值为
.(14分)
 (I)证明:在Rt△ABC中,D为AB的中点,
(I)证明:在Rt△ABC中,D为AB的中点,得AD=CD=DB,又∠B=30°,得△ACD是正三角形,
又E是CD的中点,得AE⊥CD.(3分)
折起后,AE⊥CD,EF⊥CD,
又AE∩EF=E,AE⊂平面AED,EF⊂平面AEF,
故CD⊥平面AEF,(6分)
又CD⊂平面CDB,
故平面AEF⊥平面CBD.(7分)
(II) ∵二面角A-CD-B是直二面角,
且AE⊥CD,∴AE⊥平面CBD.(8分)
连接EB,AB,则∠ABE就是直线AB与
平面CBD所成的角.(9分)
设AC=a,在△CDB中,
∠DCB=30°,CE=
| a |
| 2 |
| 3 |
∴EB2=CE2+CB2-2CE•CB•cos∠DCB=
| 7 |
| 4 |
| ||
| 2 |
| AE |
| EB |
| ||||
|
| ||
| 7 |
∴直线AB与平面CBD所成角的正切值为
| ||
| 7 |
看了 如图,在Rt△ABC中,∠A...的网友还看了以下:
r(A*A^T)=r(A^T*A)=r(A)证明方程AX=0与A^TAX=0同解AX=0显然有A^ 2020-06-10 …
曲线y=ex+e−x2与直线x=0,x=t(t>0)及y=0围成一曲边梯形.该曲边梯形绕x轴旋转一 2020-06-14 …
设f(x)为连续函数,f(0)=a,F(t)=∫∫∫Ω{z-f(x^2+y^2+z^2)]dv,其 2020-06-15 …
导数的连续性设f(x)可导,且f(0)=0,f(x)在0点的导数不为0,求w=lim(x→0){x 2020-07-16 …
设f'(x)连续,f(0)=0,f'(0)不等于0,求lim∫f(t)dt/∫f(t)dt注明x趋 2020-07-16 …
如图,在平面直角坐标系xOy中,直线y=3x,y=0,x=t(t>0)围成的△OAB的面积为S(t 2020-07-20 …
设y=f(x,t),且方程F(x,y,t)=0确定了t=t(x,y),求dy/dx457页的答案在 2020-07-22 …
∫(0→π)√(sin∧3x-sin∧5x)dx正确答案是4/5,如果令sinx=t,x=0→t= 2020-08-01 …
定义法求y=(sinx)^2的周期书上是(sin(x+T))^2-(sinx)^2=0((sin( 2020-08-02 …
一道极限的问题,t都是趋于0+第一个式子是lim(t趋于0+)(e^t-1)lnt,用等价代换(e^ 2021-01-07 …