早教吧作业答案频道 -->数学-->
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.(1)若DE∥平面A1MC1,求CEEB;(2)求证:平面B1MC1⊥平面A1MC1.
题目详情
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
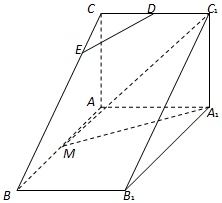
(1)若DE∥平面A1MC1,求
;
(2)求证:平面B1MC1⊥平面A1MC1.

(1)若DE∥平面A1MC1,求
| CE |
| EB |
(2)求证:平面B1MC1⊥平面A1MC1.
▼优质解答
答案和解析
(1)取BC中点为N,连结MN,C1N,
∵M,N分别为AB,CB中点∴MN∥AC∥A1C1,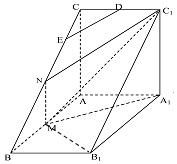
∴A1,M,N,C1四点共面,
且平面BCC1B1∩平面A1MNC1=C1N,
又DE⊂平面BCC1B1,且DE∥平面A1MC1,
∴DE∥C1N,
∵D为CC1的中点,∴E是CN的中点,∴
=
. …(6分)
证明:(2)连结B1M,
∵三棱柱ABC-A1B1C1为直三棱柱,∴AA1⊥平面ABC,
∴AA1⊥AB,即四边形ABB1A1为矩形,且AB=2AA1,
∵M是AB的中点,∴B1M⊥A1M,
又A1C1⊥平面ABB1A1,∴A1C1⊥B1M,
从而B1M⊥平面A1MC1,
∵B1M⊂平面B1MC1,∴平面B1MC1⊥平面A1MC1.…(12分)
∵M,N分别为AB,CB中点∴MN∥AC∥A1C1,

∴A1,M,N,C1四点共面,
且平面BCC1B1∩平面A1MNC1=C1N,
又DE⊂平面BCC1B1,且DE∥平面A1MC1,
∴DE∥C1N,
∵D为CC1的中点,∴E是CN的中点,∴
| CE |
| EB |
| 1 |
| 3 |
证明:(2)连结B1M,
∵三棱柱ABC-A1B1C1为直三棱柱,∴AA1⊥平面ABC,
∴AA1⊥AB,即四边形ABB1A1为矩形,且AB=2AA1,
∵M是AB的中点,∴B1M⊥A1M,
又A1C1⊥平面ABB1A1,∴A1C1⊥B1M,
从而B1M⊥平面A1MC1,
∵B1M⊂平面B1MC1,∴平面B1MC1⊥平面A1MC1.…(12分)
看了 如图,直三棱柱ABC-A1B...的网友还看了以下:
1.若正数a,b满足ab-(a+b)=1,则a+b最小值为多少?2.设M=(1/a-1)(1/b- 2020-04-05 …
数集M满足条件,若a∈M,则1+a/1-a∈M(a≠±1且a≠0.已知3∈M,请把由此确定的集合M 2020-04-06 …
如果有理数ab满足ab-2的绝对值+1-b的绝对值=0,试求:ab/1 + (a+1)(b+1)/ 2020-04-06 …
已知f(X)=Lg1-X/1+X,a,b属于(-1,1)求证:f(a)+f(B)=F(A+B)/1 2020-05-22 …
若a+m²=2004,b+m²=2003,c+m²=2002,且abc=24,求a∕bc+b∕ac 2020-05-22 …
1.m-mmX=3+1,y=9+(1/3),试求y与x的函数关系式2.已知:a+x方=2005,b 2020-06-03 …
如果有理数a,b满足|ab-2|+|1-b|=0.试求1/ab+1/(a+1)(b+1)+1(a+ 2020-07-09 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
若m、n(n<m)是关于x的一元二次方程1-(x-a)(x-b)=0的两个根,且b<a,则m,n, 2020-08-03 …
1.已知x+y=a,xy=b,用含a,b的代数式分别表示x^2+y^2,和(x-y)^2[x^2表示 2020-10-31 …