早教吧作业答案频道 -->数学-->
在平面几何的学习过程中,我们经常会研究角和线之间的关系.(1)如图①,直线a、b被直线c所截,交点分别为A、B.当∠1、∠2满足数量关系时,a∥b;(2)如图②,在(1)中,作射线B
题目详情
在平面几何的学习过程中,我们经常会研究角和线之间的关系.
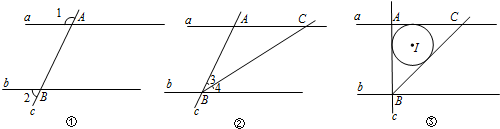
(1)如图①,直线a、b被直线c所截,交点分别为A、B.当∠1、∠2满足数量关系___时,a∥b;
(2)如图②,在(1)中,作射线BC,与直线a的交点为C,当∠3、∠4满足何种数量关系时,AB=AC?证明你的结论;
(3)如图③,在(2)中,若∠BAC=90°,AB=2, I为△ABC的内切圆.
①求 I的半径;
②P为直线a上一点,若 I上存在两个点M、N,使∠MPN=60°,直接写出AP长度的取值范围.

(1)如图①,直线a、b被直线c所截,交点分别为A、B.当∠1、∠2满足数量关系___时,a∥b;
(2)如图②,在(1)中,作射线BC,与直线a的交点为C,当∠3、∠4满足何种数量关系时,AB=AC?证明你的结论;
(3)如图③,在(2)中,若∠BAC=90°,AB=2, I为△ABC的内切圆.
①求 I的半径;
②P为直线a上一点,若 I上存在两个点M、N,使∠MPN=60°,直接写出AP长度的取值范围.
▼优质解答
答案和解析
(1)∠1+∠2=180°,
故答案为:∠1+∠2=180°;
(2)当∠3=∠4时,AB=AC,
证明:∵a∥b,
∴∠ACB=∠4,
又∵∠3=∠4,
∴∠ACB=∠3,
∴AB=AC;
(3)①由(2)得AB=AC,
又∵∠BAC=90°,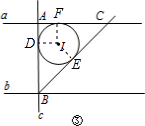
∴△ABC是等腰直角三角形.
∵AB=2,
∴AC=2.
∴在Rt△ABC中,BC=
=2
.
设D、E、F分别为边AB、BC、AC上的切点,
连接ID、IE、IF,
∵ I为△ABC的内切圆,
∴ID⊥AB、IE⊥BC、IF⊥AC.
∴AD=AF,BD=BE,CE=CF.
∵∠BAC=90°,
∴四边形ADIF是矩形.
∵ID=IF,
∴矩形ADIF是正方形.
∴r=AD=
=2-
.
∴ I的半径为2-
;
②当点P在射线AC上时,0≤AP≤2
-
+2-
,
当点P在射线AC的反向延长线上时,0≤AP≤2
-
-2+
.
故答案为:∠1+∠2=180°;
(2)当∠3=∠4时,AB=AC,
证明:∵a∥b,
∴∠ACB=∠4,
又∵∠3=∠4,
∴∠ACB=∠3,
∴AB=AC;
(3)①由(2)得AB=AC,
又∵∠BAC=90°,

∴△ABC是等腰直角三角形.
∵AB=2,
∴AC=2.
∴在Rt△ABC中,BC=
| AB2+AC2 |
| 2 |
设D、E、F分别为边AB、BC、AC上的切点,
连接ID、IE、IF,
∵ I为△ABC的内切圆,
∴ID⊥AB、IE⊥BC、IF⊥AC.
∴AD=AF,BD=BE,CE=CF.
∵∠BAC=90°,
∴四边形ADIF是矩形.
∵ID=IF,
∴矩形ADIF是正方形.
∴r=AD=
| AB+AC-BC |
| 2 |
| 2 |
∴ I的半径为2-
| 2 |
②当点P在射线AC上时,0≤AP≤2
| 3 |
| 6 |
| 2 |
当点P在射线AC的反向延长线上时,0≤AP≤2
| 3 |
| 6 |
| 2 |
看了 在平面几何的学习过程中,我们...的网友还看了以下:
设a,b是异面直线,直线a在平面α内,直线b在平面β内,且a平行β,b平行α,求证:α平行β 2020-04-05 …
在平面直角坐标系中,射线OE与x的正半轴的夹角为30°,A在OE上,A在第一象限,AB⊥x轴于点B 2020-05-16 …
设某商品的需求曲线为线性,在曲线上的A点,价格和销量分别为6元和4只,并知该点的点弹性为-3,则可 2020-05-21 …
一质点沿两个半径为R的圆弧从A运动到C,所用时间为t,求这个过程中物体的平均速率和平均速度图是中间 2020-05-23 …
高中几何证明题~有关平行~设a,b是异面直线,直线a在平面A内,直线b在平面B内,且a平行于B,直 2020-06-03 …
电磁场上每一点的()方向都跟这点的电场强度方向一致;如图所示为电场中的一条线,a点的电势()b点的 2020-06-06 …
在同一平面内,过一点可能有两条以上的直线与已知直线平行吗?任意画一条直线a,在直线外取点P,并过点 2020-06-06 …
(2010•温州模拟)如图,已知圆A过定点B(0,2),圆心A在抛物线C:x2=4y上运动,MN为 2020-06-23 …
怎么选择断链桩号拜托了各位谢谢例:某路线A在定测时,在AK2+356.400处开始局部改线,老路线 2020-06-26 …
数学:立体几何..AB是异面直线a和b的公垂线.A在a上B在b上M在a上N在b上.AB为4AM为3 2020-06-27 …